Chemia fizyczna

Jedną z gałęzi chemii fizycznej po raz pierwszy badanych była teoria powinowactwa. Słowo affinitas stosuje Albertus Magnus na określenie związku chemicznego (ok. 1250 r.). R. Boyle, J. Mayow, J. Glauber, I. Newton i G. E. Stahl przedstawiają pomysły na temat selektywnego powinowactwa. W 1718 E. F. Geoffroy umieścił substancje, w tym kwasy i zasady, w tabeli powinowactwa. Na czele kolumny znajduje się substancja, z którą wszystkie poniższe substancje mogą się łączyć. Te ostatnie są tak umieszczone, że każda substancja zastępuje wszystkie inne znajdujące się niżej w kolumnie z ich związków związkami na szczycie tabeli. Metodę tę rozszerzył T. O. Bergman (1775), chociaż konieczne było, jak wskazał A. Baumé w 1773 r., mieć dwa zestawy tabel, jeden dla reakcji w roztworze w zwykłej temperaturze, a drugi dla reakcji podczas stapiania. Bergman wskazał również, że w niektórych przypadkach konieczne jest użycie nadmiaru odczynnika, aby reakcja przebiegła do końca.

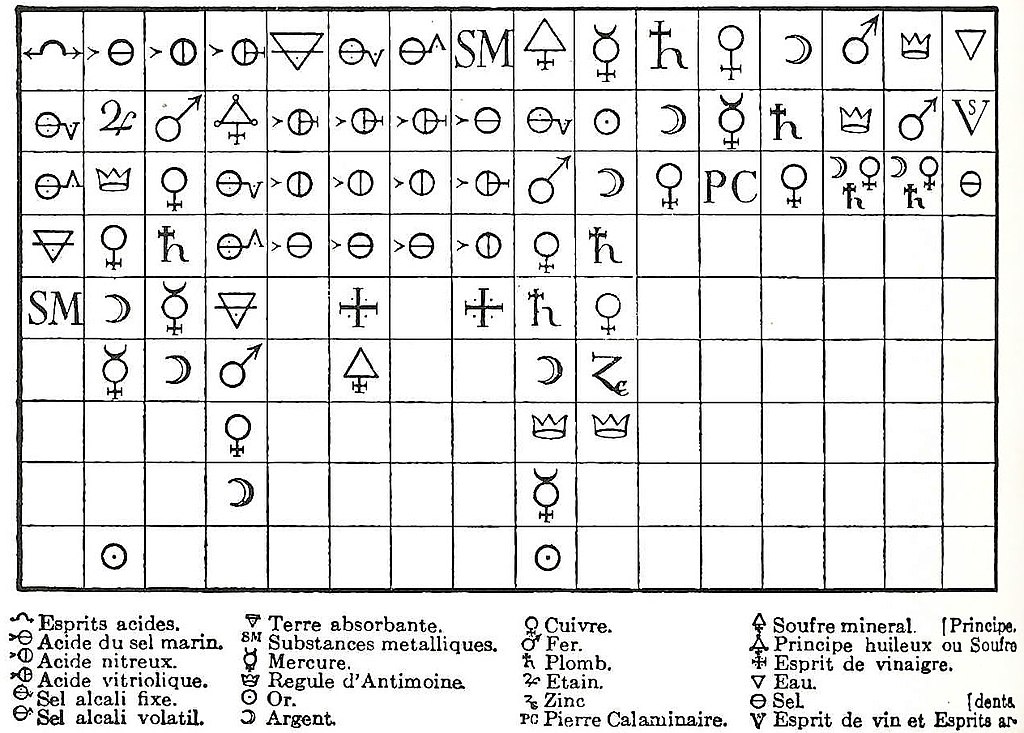Tabela powinowactwa Étienne François Geoffroy’a (1718 r.)R. Boyle w 1674 r., mówiąc o wpływie atmosfery na ciała, pisze: „Od dawna myślałem, że w różnych przypadkach ilość substancji może znacznie bardziej zrekompensować jej brak siły, niż chemicy są tego powszechnie świadomi." C. F. Wenzel w 1777 roku wpadł na pomysł, że stężenie substancji obecnych w roztworze ma wpływ na powinowactwa i wykazał, że szybkość rozpuszczania metali w kwasach jest proporcjonalna do stężenia kwasu. „Wpływ masy” został jednak po raz pierwszy wyraźnie wskazany przez C. L. Bertholleta Zwiększenie stężenia powoduje, że reakcja przebiega z większą wydajnością, chociaż reakcje zwykle nie przebiegają całkowicie w stronę produktów, ustala się stan równowagi, w którym produkty reakcji wykazują tendencję do przechodzenia z powrotem w substraty: „powinowactwa nie działają jako siły absolutne, za pomocą których substancja jest przemieszczana z jej związku, ale raczej we wszystkich kombinacjach i rozkładach. . . substancja, na którą działają dwie inne substancje z przeciwstawnymi siłami, jest między nie podzielona, ​​a stosunek podziału zależy nie tylko od wewnętrznej siły powinowactwa, ale także od ilości obecnych ciał działających, aby uzyskać równy stopień nasycenia masa można nadrobić to, czego wymaga siła powinowactwa ”. Berthollet starał się wprowadzić błędną teorię zmienności składu substancji chemicznych, co zostało obalone przez Prousta. Gay-Lussac poparł prawo działania mas, Heinricha Rose’a w 1842 r., i wykorzystał go do wyjaśnienia niektórych reakcji chemicznych, a J. J. Berzelius wskazał, że krytyka niezgodności prawa działania mas z prawem o stałych stosunkach wagowych była oparta na nieporozumieniu.

Większość ówczesnych podręczników przynajmniej wspomniała o teorii Bertholleta. Przykładowo W. Henry, po pięciu zastrzeżeniach do teorii, zauważa, że: „Niezależnie od tych zastrzeżeń do teorii Bertholleta, o ile zostały one dokonane przez autora, w wyjaśnieniu zjawisk chemicznych, nadal należy przyznać, że siły zewnętrzne, na co zwrócił uwagę ten ostry filozof, mają ogromny wpływ na modyfikację efektów powinowactwa chemicznego.” Berthollet założył, że wytwarzanie lotnych lub nierozpuszczalnych produktów może znacznie wpływać na przebieg reakcji. W 1853 r. R. Bunsen spalał mieszaniny tlenku węgla i wodoru z ilościami tlenu niewystarczającymi do całkowitego spalenia obu gazów i uzyskał ciekawy wynik, że proporcja każdego gazu łączącego się z tlenem nie zmieniała się równomiernie wraz ze zmianą stosunku gazów palnych, ale zmieniany te per saltum zachodziły w postaci całkowitych wielokrotności ale tylko dla pewnych składów mieszanin. Było to oczywiście niezgodne z teorią Bertholleta. Wyniki tym doświadczeń, jak wykazali Horstmann (1877 r.) i R. W. Dixona (1884 r.) okazały się błędne: jeśli zapobiegnie się kondensacji pary wodnej na ściankach eudiometru, wyniki są  zgodne z prawem działania mas.

W 1850 r. Ludwig Wilhelmy po raz pierwszy zbadał szybkość postępu reakcji chemicznej na przykładzie inwersji cukru trzcinowego rozpuszczonego wodzie w obecności kwasu. Ten wybór był podyktowany faktem, że postęp reakcji może być śledzony za pomocą  polarymetru, bez zakłócania warunków układu reagującego. Wilhelmy stwierdził, że w obecności dużej i praktycznie stałej masy wody ilość cukru zmieniana w krótkim przedziale czasu, dt, jest proporcjonalna do ilości cukru zawartego w danej chwili w roztworze M:

–dM/dt = kM, gdzie k jest pewną stałą; po scałkowaniu stężenie substancji M w czasie wyraża się wzorem: –logM = kt + const.

Dynamiczny charakter równowagi chemicznej, czyli. że jest ona wynikiem dwóch przeciwnych zmian zachodzących w równych proporcjach, został wskazany przez  A. W. Williamsona w 1850 roku.

W 1855 J. H. Gladstone badał reakcję:

Fe(NO₃)₃ + 3KCNS → Fe(CNS)₃ + 3KNO₃, której przebieg można określić na podstawie głębokości koloru roztworu ze względu na tworzony czerwony rodanek żelaza(III). Jak zaobserwował tworzy się stan równowagi: „zmiana masy jednego z dwuskładnikowych związków powoduje zmianę ilości każdego z pozostałych dwuskładnikowych związków, i to w regularnie postępującym stosunku”.

W tym zakresie niezwykle istotne są badania C. L. Berthelota i P. de Sainte-Gillesa  (1862-3), którzy badali reakcję:

alkohol + kwas ↔ ester + woda.

Reakcja ta nigdy nie zachodzi do końca, ale powoli zbliża się do granicy odpowiadającej równowadze. Tę samą równowagę osiąga się niezależnie od tego, czy bada się mieszaninę alkoholu i kwasu czy estru i wody. „Ilość estru powstającego w każdym momencie jest proporcjonalna do iloczynu stężeń reagujących substancji i odwrotnie proporcjonalna do objętości.” Chociaż udało im się wydedukować matematyczne wyrażenia dotyczące prędkości reakcji, Berthelot i Sainte-Gilles nie opracowali prawa działania mas, jak to zostało później sformułowane przez C. Guldberga i P. Waage’a, ponieważ nie uwzględnili szybkości reakcji odwrotnej między estrem i wodą, chociaż wiedzieli, że taki proces zachodzi.

W latach 1866-7 W. V. Harcourt i W. Esson, w Oksfordzie, próbowali uzyskać informacje o przebiegu przemiany chemicznej badając reakcję: 2HI + H₂O₂ → 2H₂O +I₂, w obecności rozcieńczonego kwasu siarkowego. Badali również redukcję manganianu(VIII) potasu przez kwas szczawiowy w obecności rozcieńczonego kwasu siarkowego(VI) i siarczanu(VI) manganu(II). Jest to kolejna reakcja, w której substancja A jest przekształcana w substancję pośrednią M, która następnie tworzy substancję końcową B. Ustalili i rozwiązali równania różnicowe dla badanych reakcji.

Prawo działania mas zostało po raz pierwszy ogłoszone  w formie ogólnej przez C. Guldberga i P. Waage'a, odpowiednio profesorów matematyki stosowanej i chemii, na University of Christiania (Oslo). W 1864 roku ukazał się ich pierwszy artykuł w języku norweskim; pełny tekst w języku francuskim został opublikowany w 1867 r. Wskazują oni, że podobnie jak w mechanice „musimy badać reakcje chemiczne, w których siły wytwarzające nowe związki są utrzymywane w równowadze przez inne siły … gdzie reakcja nie jest zakończona, ale tylko częściowa ”.

Zdefiniowali „masę aktywną” jako liczbę cząsteczek w jednostkowej objętości. Kiedy „dwie substancje A i B są przekształcane przez podwójne podstawienie w dwie nowe substancje A' i B', i w tych samych warunkach A' i B' mogą przekształcić się w A i B ... siła, która powoduje utworzenie A’ i B’ wzrasta proporcjonalnie do współczynników powinowactwa reakcji A + B = A’ + B’, ale zależy również od mas A i B. Z naszych eksperymentów dowiedzieliśmy się, że siła jest proporcjonalna do iloczynu mas czynnych dwóch substancji A i B. Jeżeli oznaczymy masy aktywne A i B przez p i q, a współczynnik powinowactwa przez k, siła = k·p·g.” Nie jest to jednak jedyna siła wpływająca na przebieg reakcji. „Niech aktywne masy A’ i B' będą p’ i g', a współczynnik powinowactwa reakcji A'+ B' = A + B oznaczmy k'. Siła powodująca ponowne tworzenie A i B będzie wynosić k'·p'·q’. Siła ta jest w równowadze z pierwszą, a zatem k·p·q = k'·p'·q’. Określając eksperymentalnie aktywne masy p, q, p' i q’, możemy znaleźć stosunek między współczynnikami k i k’. Z drugiej strony, jeśli znaleźliśmy stosunek k/k', możemy obliczyć wynik reakcji dla dowolnego pierwotnego stanu czterech substancji.”

J. van’t Hoff (1877) zastąpił nieokreśloną „siłę” prędkością reakcji. Prędkość, z jaką A i B reagują tworząc A' i B', będzie wynosić v = k·p·q, a prędkość, z jaką A' i B' tworzą A i B, będzie wynosić v' = k'·p'·q’. Rzeczywista prędkość całej reakcji będzie wynosić V = v - v' = k·p·q – k'·p'·q’. W równowadze V = 0, a p'·q’/ p·q = k/k'.

Termochemia

Badanie powinowactwa w innym aspekcie znalazło swoje przedstawienie w próbach określenia miary sił chemicznych przez ilość ciepła wydzielonego w reakcji chemicznej. Znaczenie zjawisk termicznych w reakcjach chemicznych wyraźnie uświadomili sobie A. Lavoisier i P. S. Laplace, którzy położyli podwaliny pod termochemię. Wykazali, że ciepło powstające w reakcji jest równe ciepłu pochłoniętemu w reakcji odwrotnej. Badali specyficzne i utajone ciepło wielu substancji oraz ilości ciepła wydzielanego podczas spalania. W 1840 r. G. Hess ogłosił prawo, że wymiana ciepła w reakcji jest taka sama, bez względu na to, czy proces przebiega w jednym czy w kilku etapach. Zatem ciepło tworzenia CO₂ jest sumą ciepła powstawania CO i ciepła utleniania CO do CO₂. Tylko ilości ciepła oddane w pierwszej i trzeciej z tych zmian można zmierzyć eksperymentalnie, ale prawo Hessa pozwala nam obliczyć ciepło wymieniane w drugim etapie.

Wraz z pojawieniem się mechanicznej teorii ciepła prawo Hessa było postrzegane jako konsekwencja prawa zachowania energii. Badaniem termochemii zajął się S. Andrews oraz P. A. Favre i J. Th. Silbermann., ale głównie Berthelot w Paryżu i Julius Thomsen w Kopenhadze. Obydwoje uważali ciepło wydzielane podczas powstawania związku chemicznego za miarę powinowactwa lub pracę wykonaną przez siły chemiczne. Jednak rozważenie drugiego prawa termodynamiki, ogłoszonego przez N. Carnota w 1824 r., doprowadziło H. Helmholtza w 1882 r. do dokładniejszego oszacowania pracy wykonanej przez siły chemiczne. Nie jest to ciepło wydzielane w reakcji, ale największa ilość pracy, jaką można uzyskać, gdy reakcję prowadzi się w sposób odwracalny, np. praca elektryczna w ogniwie odwracalnym. Ta maksymalna praca jest uważana za miarę wolnej lub dostępnej energii układu, podczas gdy wydzielane ciepło jest zwykle miarą obniżenia całkowitej energii systemu.

Zastosowanie drugiej zasady termodynamiki do chemii, zapoczątkowane przez A. F. Horstmanna w 1873 r., jest istotne przy badaniu zjawisk dysocjacji. Chociaż znane były pojedyncze przykłady zmian chemicznych wywołanych przez ciepło, które ulegały odwróceniu podczas chłodzenia, głównie praca H. E. Deville’a skupiła uwagę na tym ważnym typie reakcji chemicznej. Deville był w stanie za pomocą skonstruowanego przez siebie aparatu zbadać dysocjację pary, dwutlenku węgla, dwutlenku siarki, chlorowodoru i tlenku węgla w wysokich temperaturach. Wcześniejsze eksperymenty F. J. Pebala (1862) i A. K. Thana (1864) dotyczące dysocjacji salmiaku usunęły rzekomy wyjątek od zasady Avogadra, wynikający z faktu, że gęstość par tej substancji była tylko o połowę mniejsza niż masa cząsteczkowa. Wykazano, że para jest tak naprawdę mieszaniną amoniaku i chlorowodoru, zajmując podwójną objętość niezdysocjowanej substancji: NH₄C1 → NH₃ + HC1. S. Cannizzaro w 1857 r. oraz H. M. F. Kopp i A. Kekulé 1858 wskazali, że wszystkie tak zwane wyjątki to przypadki, w których dochodzi do dysocjacji.

H. E. Deville i J. H. Debray (1867–8) wykazali, że w wielu przypadkach, w których substancja stała ulega zdysocjowaniu, np. CaCO₃ → CaO + CO₂, ciśnienie formy zdysocjowanej zależy tylko od temperatury, a nie od ilości obecnych substancji. Uznano to za wyjątek od prawa działania mas, ale przypadek, w którym układ nie jest jednorodny, wymaga specjalnego traktowania, a wyjątek jest tylko pozorny. H. J. Horstmann wskazał, że ten przypadek, i niektóre inne badane przez niego, są analogiczne do procesu fizycznego przemiany stanu, i że stosuje się tu również równanie termodynamiczne wyprowadzone przez Clapeyrona i Clausiusa czyli dp/dT = Q/T(v’ – v), gdzie p to ciśnienie, Q ciepło dysocjacji, T temperatura absolutna, a v' i v objętości układu po i przed dysocjacją. Jeśli powstały gaz lub pary mają zachowywać się jak gaz idealny, a objętość ciał stałych jest zaniedbywalna w porównaniu z objętością gazów, równanie przyjmuje postać: dlogp/dT = Q/RT², gdzie R jest stałą gazową dla cząsteczki o masie 1 grama. J. van’t Hoff w latach 1884–6 uogólnił to równanie, tak by można je było stosować do wszystkich przypadków równowagi chemicznej między gazami lub substancjami w roztworach rozcieńczonych. W tym przypadku stała równowagi K zastępuje p w powyższym równaniu. Całkowanie tego równania daje możliwość znalezienia Q na podstawie pomiarów wpływu temperatury na K, ale problem obliczenia K na podstawie ciepła reakcji Q nie został rozwiązany, ponieważ całkowanie wprowadza nieokreśloną stałą (całkowania): logK = –Q/RT + const. W. Nernst w 1906 r. wykazał, że przyjmując inne założenie, można było obliczyć wartość tej stałej, a problem znalezienia K, a tym samym powinowactwa z ciepła reakcji, został rozwiązany.

Reguła faz

W układach, które nie są jednorodne, najbardziej użytecznym narzędziem do ich opisu jest reguła faz Willarda Gibbsa, ogłoszona w 1876 r. Artykuł Gibbsa o równowadze w układach heterogenicznych został opublikowany w mało znanym amerykańskim czasopiśmie (Trans. Connecticut Acad., 1875-6, III, 152 (January, 1876)); wspomniał o nim J. Clerk Maxwell w swojej Theory of Heat, ale sam tekst pozostał praktycznie niezauważony do 1884 r., kiedy H. W. B. Roozeboom, pracujący w laboratorium van Bemmelena w Lejdzie nad hydratami dwutlenku siarki, zwrócił na niego uwagę van der Waalsa, profesora fizyki. Reguła dotyczy układów zawierających dwa lub więcej ciał zwanych fazami, oddzielonych granicami, np. ciecz i gaz lub ciecz i ciało stałe. Układ można zbudować z pewnej minimalnej liczby substancji chemicznych zwanych składnikami. Zatem woda i dwutlenek siarki były składnikami w przypadku układu Roozebooma. Aby układ był w równowadze, muszą być spełnione pewne warunki temperatury, ciśnienia i stężenia w różnych fazach. Liczba tych zmiennych, które muszą zostać ustalone przed osiągnięciem równowagi, nazywana jest liczbą stopni swobody układu. Jeśli P jest liczbą faz, C liczbą składników, a F liczbą stopni swobody, to Gibbs wykazał, że P + F = C + 2.

Roztwory

Podstawowe badania, na których oparta jest teoria roztworów, to prace Raoulta i Pfeffera.

François-Marie Raoult urodził się w 1830 roku w Fournes, w Département du Nord we Francji. W 1853 r. otrzymał stanowisko nauczyciela w Lycee w Rheims, i po podjęciu dodatkowych prac był w stanie opłacić studia i uzyskać stopień naukowy w 1863 roku. Jego prace badawcze dotyczyły ciepła reakcji i sił elektromotorycznych ogniw galwanicznych,  zauważył, że ciepło reakcji nie jest równoważne powinowactwu chemicznemu, tak jak sugerowała to teoria. W 1867 r. zatrudnił się na uniwersytecie w Grenoble na stanowisku asystenta na wydziale chemicznym, a w 1870 r. awansował na stanowisko profesora. Pozostał w Grenoble do śmierci w 1901 r.

W 1878 r. ukazała się pierwsza publikacja Raoulta na temat krzepnięcia roztworów. Do badań używał głównie substancji organicznych i w wyniku wielu pomiarów w 1882 r. był w stanie opublikować zestawienie, z którego wynikało, że iloczyn wielkości wartości obniżenia temperatury krzepnięcia roztworu zawierającego 1 gram substancji w 100 gramach wody przez masę cząsteczkową substancji jest wartością stałą. „To wskazuje na dowód, że w większości przypadków cząsteczki związków organicznych są po prostu oddzielane przez akt rozpuszczania i doprowadzane do tego samego stanu, w którym wywierają taki sam wpływ na właściwości fizyczne wody.” Było również jasne, że ciężary cząsteczkowe rozpuszczonych substancji można wyznaczyć na podstawie temperatur krzepnięcia roztworów. Jeśli C jest wartością obniżenia temperatury krzepnięcia wywołaną przez P gramów substancji w 100 gramach rozpuszczalnika, wówczas C·M/P = K, gdzie M jest masą cząsteczkową, a K stałą reprezentującą wartość C.

W 1884 r. Raoult stwierdził, że „w przeciwieństwie do tego, co do tej pory uważałem, ogólny opis krzepnięcia nie stosuje się do soli rozpuszczonych w wodzie ... wręcz przeciwnie, dotyczy rodników tworzących sole, tak jakby rodniki te były po prostu zmieszane z roztworem”. Raoult badał również ciśnienia par roztworów i wykazał w latach 1886–7, że: „jedna cząsteczka substancji nie będącej solą, rozpuszczając się w cząsteczkach 100 dowolnej lotnej cieczy, zmniejsza ciśnienie par cieczy o stały ułamek jego wartości wynoszący prawie 0,0105. ” To odkrycie stanowi podstawę metody pozwalającej na wyznaczenie ciężarów cząsteczkowych substancji w roztworze, chociaż E. O. Beckmann w 1889 r. wykazał, że wygodniej jest mierzyć zmiany temperatury wrzenia lub krzepnięcia.

Wilhelm Pfeffer prowadził innym rodzaju badania zajmując się ciśnieniem osmotycznym. Od początku XVIII wieku było wiadomo, że gdy roztwór zostanie oddzielony od czystej wody membraną, taką jak pęcherz, woda przenika przez membranę i rozcieńcza roztwór, wywierając ciśnienie, jeśli zapobiega się zwiększeniu objętości tego drugiego. Ciśnienie to nazwano ciśnieniem osmotycznym. W 1877 r. Pfeffer był w stanie, osadzając żelazocyjanek miedzi w ściankach porowatego naczynia, przygotować membrany, które przepuszczały wodę, ale nie przepuszczały rozpuszczonego cukru. Za pomocą tych półprzepuszczalnych membran zmierzył ciśnienie osmotyczne roztworów. Jego wyniki, za wyjątkiem botaników, nie były ogólnie znane, a uwagę van’t Hoffa zwrócił na nie jego kolega J. de Vries, profesor botaniki. Van’t Hoff od razu docenił ich wielkie znaczenie. W 1886 r. wykazał na podstawie wyników Pfeffera, że ​​ciśnienie osmotyczne wywierane przez rozpuszczoną substancję jest równe ciśnieniu, jakie wywierałoby ono jako gaz zamknięty w przestrzeni równej objętości roztworu; „Stopniowo wydawało się, że istnieje podstawowa analogia, a właściwie prawie tożsamość, z gazami, szczególnie w aspekcie fizycznym, choć tylko w roztworach rozważamy tak zwane ciśnienie osmotyczne zamiast zwykłego ciśnienia gazowego ... nie mamy tu do czynienia z fantazyjną analogią, ale z czymś fundamentalnym”. Dzięki zastosowaniu zasad termodynamiki van't Hoff był w stanie określić ilościowy związek między ciśnieniem osmotycznym a obniżeniem temperatury krzepnięcia lub obniżeniem ciśnienia par roztworu.

Raoult odnotował trudności z roztworami soli w wodzie. Wykazywały one wyższe ciśnienie osmotyczne niż można by oczekiwać na podstawie teorii van’t Hoffa. Analogicznie do dysocjacji gazów możemy spodziewać się pewnego rodzaju dysocjacji soli w roztworze. Planck w 1887 r. również założył dysocjację soli na rodniki, ale pełne wyjaśnienie zjawiska zostało podane w elektrolitycznej teorii dysocjacji Arrheniusa. Teoria dysocjacji elektrolitycznej opierała się na fakcie, że roztwory wykazujące anormalnie wysokie ciśnienia osmotyczne były przewodnikami elektryczności.

Dysocjacja elektrolityczna

Svante Arrhenius urodził się w 1859 r. w Wijk, niedaleko Uppsali w Szwecji, studiował w Uppsali, Sztokholmie i Rydze (u Ostwalda). Następnie pracował w Niemczech, i z van’t Hoffem w Amsterdamie. W 1891 r. został mianowany wykładowcą, a w 1895 r. profesorem fizyki na politechnice w Sztokholmie. Otrzymał Nagrodę Nobla w 1903 roku, a po odrzuceniu zaproszenia do Berlina był dyrektorem Instytutu Nobla w Sztokholmie od 1905 roku aż do swojej śmierci w 1927 roku.

J. W. Hittorf w latach 1853-59 wykazał, stosując elektrolizer własnej konstrukcji, , że zmiany stężenia w obu przestrzeniach przyelektrodowych nie są jednakowe, co można wyjaśnić, przypisując różnym jonom niejednakowe zdolności do transportowania ładunku elektrycznego przez dany roztwór (różne ruchliwości, od których zależą udziały w przenoszeniu ładunków, nazwane „liczbami przenoszenia”).

Friedrich W. G. Kohlrausch w 1874 r. wykazał, że przewodnictwo równoważnikowe, tzn. przewodnictwo właściwe κ podzielone przez stężenie roztworu wyrażone w równoważnikach na cm³, κ/c = L, mocno rozcieńczonego roztworu soli, jest sumą dwóch czynników, jednego zależnego tylko od kationu, a drugiego tylko od anionu: L = l_a + l_k. l_a i l_k nazywane są ruchliwościami jonów. Jeśli n jest liczbą przenoszenia Hittorfa, to l_a = n·L.

W połączeniu z wynikami Raoulta wydawało się to wskazywać na dysocjację soli na dwa jony w roztworze – tak zwaną jonizację. Działanie prądu elektrycznego polega jedynie na skierowaniu dodatnio i ujemnie naładowanych jonów w kierunku elektrod o przeciwnych znakach. Ponieważ liczba naładowanych cząstek w danej objętości jest zwiększana przez jonizację, wyjaśniono nienormalnie wysokie ciśnienia osmotyczne i związane z nimi anormalne obniżenia temperatury krzepnięcia. Arrhenius był w stanie wykazać, że stopień jonizacji obliczony na podstawie przewodności elektrycznej, L/L_∞, gdzie L_∞ jest przewodnością równoważnikową przy nieskończonym rozcieńczeniu (przy całkowitej jonizacji), był bardzo zbliżony do obliczonego na podstawie odchyleń od prawa Raoulta w przypadku pomiarów temperatury krzepnięcia. Są to dwie niezależne metody i w ten sposób ustalono istotną poprawność teorii. Współczesne badania zmodyfikowały teorię Arrheniusa pod pewnymi względami, ponieważ silne kwasy, zasady i sole są praktycznie całkowicie zjonizowane w silnie rozcieńczonych roztworach, a odchylenia od całkowitej jonizacji przypisuje się oddziaływaniu jonów o przeciwnych znakach, które powoduje zmniejszenie ich ruchliwości, a tym samym zmniejszenie L (P. Debye, E. Hūckel, 1923).

Teoria dysocjacji elektrolitycznej początkowo nie została przyjęta przez większość chemików, którzy nie mogli zrozumieć, jak na przykład sód i chlor mogą znaleźć się w roztworze zwykłej soli. W 1885 r. H. E. Armstrong zaproponował teorię przemian chemicznych, według której wszystkie procesy miały charakter elektrolityczny, i jako przykłady „odwróconej elektrolizy”. Reakcje przebiegały między trzema ciałami, z których przynajmniej jedno musi być elektrolitem. Zatem w reakcji łączenia wodoru i tlenu gazy działały jak elektrody, a woda, która musi być przy tym obecna, działała jak elektrolit:

2H₂ + 2O:H₂ + O₂ → 2H2O + 2H2O.

H. E. Armstrong, jednym z głównych przeciwników teorii jonizacji Arrheniusa, zakładał, że skoro czysta woda prawie nie przewodzi elektryczności, musi istnieć pewne zanieczyszczenie, która sprawia, że pojawia się przewodnictwo.

Jednym z głównych orędowników nowych teorii roztworów był Wilhelm Ostwald (1853–1932), profesor w Lipsku. Ostwald wcześniej przeprowadził badania nad powinowactwem i działaniem mas, i z entuzjazmem przyjął poglądy Arrheniusa. Był doskonałym nauczycielem, a w swoich wykładach i podręcznikach popularyzował teorię dysocjacji elektrolitycznej pokazując, jak można ją zastosować w wyjaśnianiu reakcji chemicznych, w tym w chemii analitycznej.

Istotnego rozszerzenia teorii Arrheniusa dokonał Walther Nernst (1864–1941), najpierw asystent Ostwalda, a następnie profesor w Getyndze i Berlinie. W 1889 r. wykazał, że wytwarzanie siły elektromotorycznej w ogniwach galwanicznych można wyjaśnić w kategoriach „ciśnienia roztworu” elektrod metalowych, które dążą do przeprowadzenia naładowanych jonów do roztworu, a tendencję tę równoważy ciśnienie osmotyczne rozpuszczonych jonów. Nernst wprowadził także w 1889 r. teorię iloczynu rozpuszczalności, wyjaśniającą reakcje strącania. Jego podręcznik, Theoretical Chemistry from the Standpoint of Avogadro’s Rule and Thermodynamics (1893 i późniejsze wydania) zawiera bardzo dobre przedstawienie tematu.

Nernst (1906 r.) założył, że zasada Thomsena-Berthelota, zgodnie z którą ciepło reakcji U jest równe maksymalnej pracy lub powinowactwu A, jest spełnione dla reakcji między czystymi ciałami stałymi w pobliżu zera absolutnego. Lord Kelvin (1855) i H. Helmholtz (1882) wykazali, że A i U są powiązane równaniem A – U = T(dA/dT), a dla takich reakcji twierdzenie Nernsta dotyczące ciepła lub trzecie prawo termodynamiki zapewnia, że dA/dT dąży do zera w punkcie zera absolutnego. Jest to równoważne stwierdzeniu, że zmiana entropii wynosi zero, a Planck (1911 r.) założył, że entropia każdej czystej substancji stałej wynosi zero w temperaturze zera absolutnego. Oznacza to, że jego ciepło właściwe zanika przy T = 0, co eksperymentalnie potwierdził Nernst. Einstein (1907) i Debye (1913) podali równania oparte na teorii kwantów, które uzasadniają taki wynik. Nernst (1914) założył, że ciepło właściwe gazu powinno również zanikać blisko zera absolutnego.

Nernst (1906) wykazał, że twierdzenie o cieple można zastosować do obliczenia stałej całkowania równania van’t Hoffa dla stałej równowagi reakcji gazowej. Odbywa się to za pomocą entropii gazów, zliczanej od wartości dla ciał stałych w temperaturze zera absolutnego (można je również obliczyć na podstawie danych spektroskopowych).

Einstein (1912) wyjaśnił reakcje fotochemiczne, zakładając, że kwant e pochłoniętej energii promieniowania dysocjuje jedną cząsteczkę reagującego gazu. W fotochemicznej reakcji pomiędzy wodorem i chlorem (badanej przez Bunsena i Roscoe, 1855 i nast.) wydajność chlorowodoru jest znacznie większa niż można by oczekiwać na podstawie warunków reakcji. Nernst (1918) wyjaśnił to, zakładając, że cząsteczka chloru jest dysocjowana zgodnie z prawem Einsteina, ale atomy chloru wywołują „reakcję łańcuchową”, która zachodzi bez udziału światła, do momentu aż atomy nie zostaną usunięte przez zderzenie ze ścianą naczynia lub z innymi cząsteczkami gazu w mieszaninie.