Podwójna warstwa elektryczna

U podstaw zrozumienia zjawisk i procesów elektrochemicznych zachodzących na granicach międzyfazowych leży poznanie rozkładu ładunków, a tym samym rozkładu potencjału elektrycznego w tych obszarach. Modelem przybliżającym strukturę elektryczną tego obszaru jest model podwójnej warstwy elektrycznej. Układy, w których występuje podwójna warstwa elektryczna są bardzo rozpowszechnione poczynając od powierzchni roztworów wodnych soli, przez półprzewodniki graniczące z fazą gazową, metale lub izolatory zanurzone w odpowiednich roztworach do granic dwu faz ciekłych lub stałych.

Zasadniczymi czynnikami determinującymi strukturę podwójnej warstwy elektrycznej są natura pozostających w kontakcie faz oraz stan ich polaryzacji. O tym jak rozłoży się ładunek elektryczny w warstwie decyduje w znacznej mierze przewodnictwo elektryczne graniczących ośrodków, a więc rodzaj, ruchliwość i stężenie obecnych w obu fazach, lub mogących w nich powstawać, ładunków elektryczności. Ponadto adsorpcja i orientacja cząsteczek polarnych oraz indukowanie się w nich ładunków wpływają na rozkład potencjału w obszarach międzyfazowych. Z tego względu struktura podwójnej warstwy elektrycznej jest silnie uzależniona od właściwości elektrochemicznych materiałów , z których zbudowane są fazy. W metalach nośnikami ładunki są elektrony, a ich stężenia i ruchliwość są znaczne. W półprzewodnikach w zależności od rodzaju nośnikami ładunku mogą być elektrony lub "dziury", względnie jony. Stężenia tych nośników są znacznie mniejsze niż w metalach, a ponadto znajdują się w pasmach energetycznych rozdzielonych strefą wzbronioną o różnej szerokości warunkującej łatwość przewodzenia prądu. W roztworach nośnikami ładunków są jony, różniące się stopniem solwatacji i ruchliwością. Globalne stężenie jonów zależy od typu, stężenia i stopnia dysocjacji obecnych w roztworze elektrolitów. Dalsze rozważania dotyczyć będą podwójnej warstwy elektrycznej na granicy faz elektroda metaliczna – roztwór elektrolitu. Jednak zachowanie takiego układu również jest uzależnione od szeregu czynników. Dla uproszczenia zajmiemy się podwójną warstwą elektryczną sprowadzoną do modelu dwu równoległych płaszczyzn obsadzonych nośnikami przeciwnych ładunków elektrycznych, przyjmując, że ładunki te są równomiernie rozmieszczone na płaszczyznach, z których jedna pokrywa się z powierzchnią metalu, a druga znajduje się w roztworze.

Przyczyny separacji ładunków na granicy faz mogą być różne, ale najbardziej jednym z najczęstszych jest polaryzacja zewnętrzna elektrod metalowych w roztworach, w których nie mogą zachodzić procesy elektrodowe, zmienia gęstość powierzchniową elektronów w metalu co pociąga za sobą utworzenie w przylegającym do elektrody elektrolicie podwójnej warstwy elektrycznej w postaci kompensującego ładunku przestrzennego (układ musi być elektrycznie obojętny). Przykładem takiego powstawania warstwy podwójnej jest układ jaki tworzy rtęć w wodnym roztworze KJ.

Rozkład ładunków i przebieg potencjału przy samej powierzchni w głąb roztworu elektrolitu bez uwzględnienia adsorpcji jonów dla roztworów stężonych i rozcieńczonych.

W przypadku roztworów stężonych o rozkładzie ładunków decydują tylko siły oddziaływań elektrostatycznych modyfikowane ruchami cieplnymi jonów (zakładamy brak adsorpcji specyficznej). W przypadku roztworów rozcieńczonych w obszarze przylegającym do elektrody rtęciowej spadek potencjału wraz z odległością jest znacznie wolniejszy niż w roztworze o dużym stężeniu nośników ładunku.

W okolicy powierzchni rtęci, w rozcieńczonym roztworze KJ występuje silna adsorpcja specyficzna (nie elektrostatyczna) jonów jodkowych, która powoduje, że nawet przy ujemnie naładowanej powierzchni metalu mogą gromadzić się aniony.

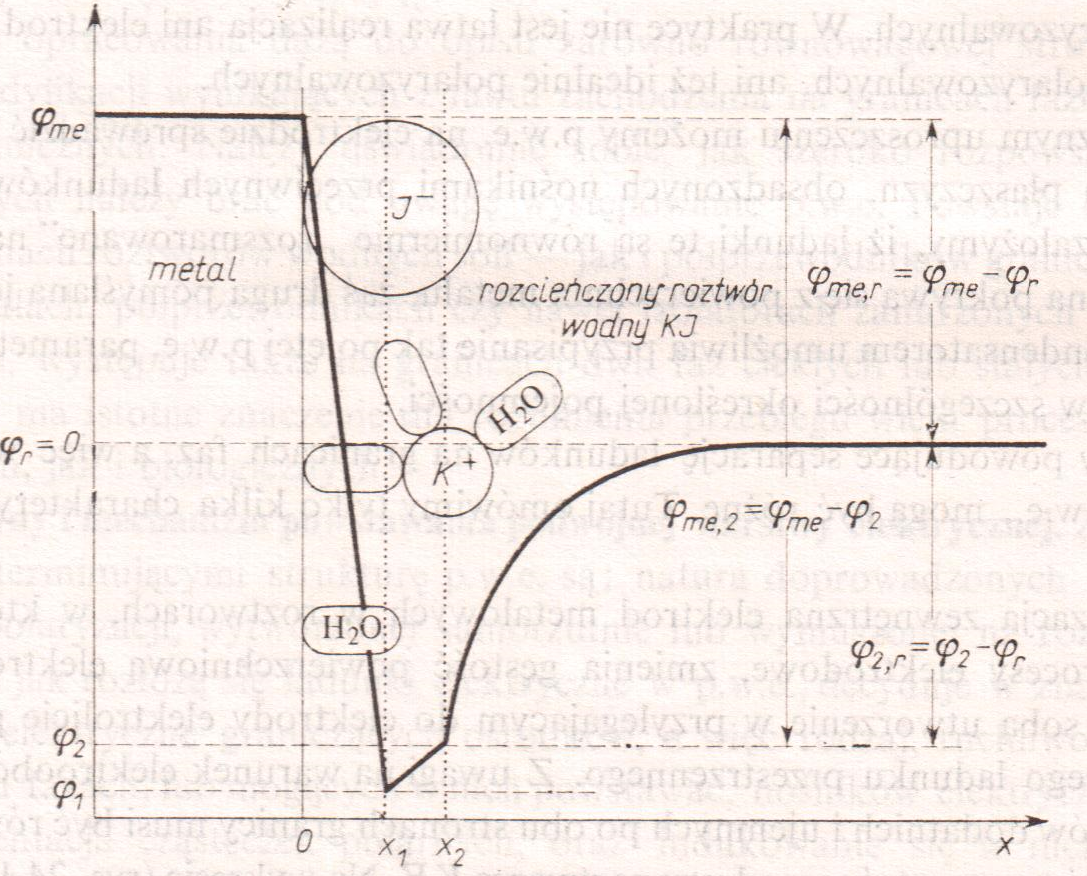Rozkład ładunku i przebieg potencjału w rozcieńczonym roztworze elektrolitu, którego aniony mogą ulegać specyficznej adsorpcji.

Podwójna warstwa elektryczna powstaje również gdy kryształ jonowy zostaje zanurzony w roztworze zawierającym jony wchodzące  skład jego sieci krystalicznej. Wspólne jony mogą ulec wbudowaniu w powierzchnię kryształu w stopniu uzależnionym od aktywności jonów w roztworze. Powoduje to zmianę gęstości powierzchniowej ładunku ciała stałego, zmianę rozkładu i wartości potencjału w obszarze przy powierzchni, czyli zmianę struktury rozkładu ładunku w roztworze.

Kolejnym przykładem powstawania podwójnej warstwy elektrycznej jest kryształ półprzewodnikowy zanurzony w roztworze lub pozostający w kontakcie z faza gazową, co może powodować powierzchniowe utlenianie. Proces ten prowadzi w konsekwencji do separacji elektronów i defektów powodując pojawienie się naładowanych stanów powierzchniowych. Natura i stężenie tych stanów decyduje o strukturze powstającej podwójnej warstwy elektrycznej. Pojawiający się w półprzewodniku obszar ładunku przestrzennego może być znacznie większy niż w rozcieńczonym roztworze wodnym.

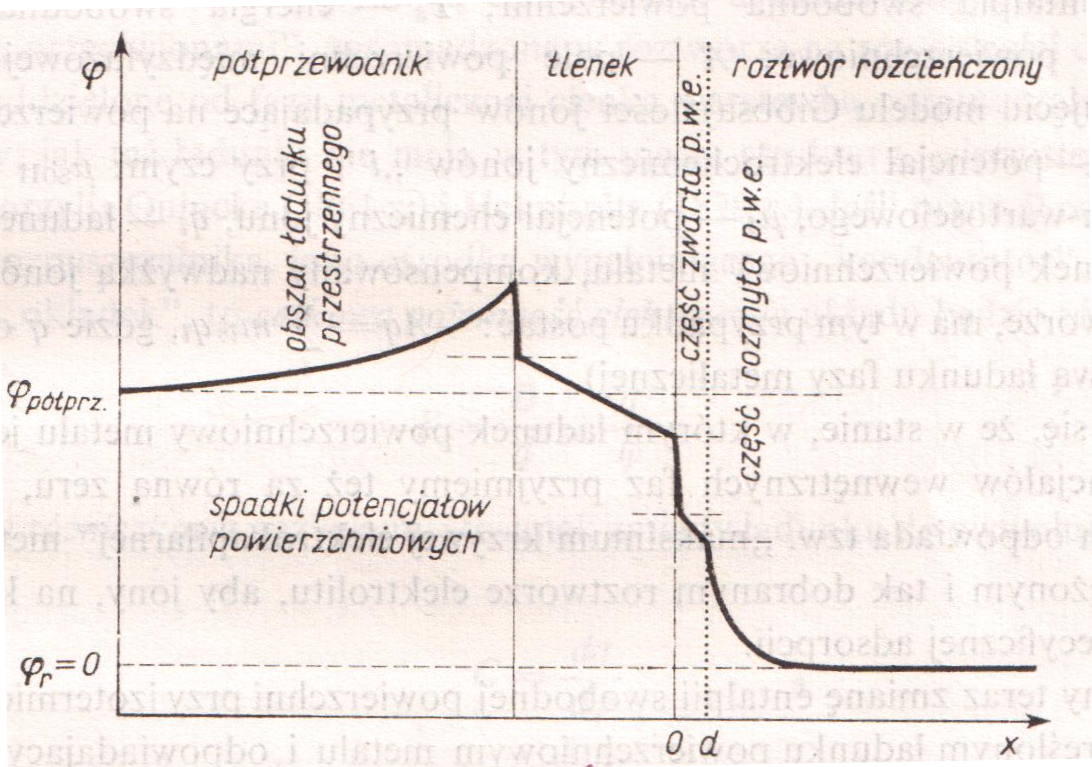Schemat przebiegu potencjału w układzie półprzewodnik ze zmienioną chemicznie, utlenioną powierzchnią - roztwór elektrolitu.

Innym procesem powodującym pojawienie się podwójnej warstwy elektrycznej jest wybiórcza adsorpcja jednego rodzaju jonów (aniony elektrolitu lub długołańcuchowe kationy organiczne) co pociąga za sobą zmianę gęstości powierzchniowej ładunku. Wreszcie kolejna przyczyną może być orientacja dipoli w obszarach międzyfazowych prowadząca do zmiany rozkładu ładunków. Szczególną rolę odgrywa w takich procesach woda, której cząsteczki odznaczają się wysokim momentem dipolowym.

Termodynamiczne ujęcie podstaw elektrokapilarności

Pomimo różnych przyczyn powstawania podwójnej warstwy elektrycznej ogólne prawidłowości i konsekwencje termodynamiczne można sformułować na gruncie nadmiarowych funkcji termodynamicznych. Rozważmy wyprowadzenie równania Lipmanna dla przykładu elektrody idealnie polaryzowalnej. W formie przybliżonej interesuje nas tylko zmiana skoku potencjału na pojedynczej granicy fazowej, a nie niemierzalna, bezwzględna wartość różnicy wewnętrznych potencjałów graniczących ośrodków.

Wychodzimy od definicji entalpii swobodnej powierzchni, nie mającej w modelu Gibbsa grubości, czyli o objętości zerowej:

gdzie G_s - entalpia swobodna powierzchni; F_s - energia swobodna powierzchni; σ - napięcie powierzchniowe; A - pole powierzchni międzyfazowej; m_is - nadwyżkowe w ujęciu Gibbsa ilości jonów przypadające na powierzchnię o polu A; ū_i =  μ_i + q_iφ - potencjał elektrochemiczny jonów "i", przy czym μ_soli = μ₊ + μ_– dla elektrolitu z -wartościowego, μ_i - potencjał chemiczny jonu, q_i - ładunek jonu. Wyrażenie na ładunek powierzchniowy metalu, kompensowany nadwyżką jonów przeciwnego znaku w roztworze ma w tym przypadku postać:

gdzie q oznacza gęstość powierzchniową ładunku fazy metalicznej.

Przyjmijmy, że w stanie, w którym ładunek powierzchniowy metalu jest równy zeru różnica potencjałów wewnętrznych faz również wynosi zero, czyli: φ = 0. Stan taki będzie odpowiadał tzw. maksimum krzywej elektrokapilarnej metalu zanurzonego w dość stężonym i tak dobranym roztworze elektrolitu, aby jony na które dysocjuje nie ulegały specyficznej adsorpcji.

Rozpatrzmy teraz zmianę entalpii swobodnej powierzchni przy izotermicznym przejściu do stanu o określonym ładunku powierzchniowym metalu i odpowiadającym, różnym od zera potencjale, ale przy nie zmienionym składzie wnętrza roztworu. Oznaczając indeksami ○ parametry odnoszące się do stanu początkowego otrzymujemy:

Całkując dla ustalonych A i T równanie Gibbsa:

i rozpisując dla powyższej różnicy stanów, otrzymujemy:

Uwzględniając kombinację powyższych równań oraz równość:

można podać całkową formę równania Lipmanna:

chociaż częściej podaje się w formę różniczkową:

Rozwój poglądów na strukturę podwójnej warstwy elektrycznej

Najprostszym, zastosowanym powyżej, modelem podwójnej warstwy elektrycznej jest płaski kondensator, którego jedną okładkę tworzy powierzchnia metalu z obsadzającymi ją elektronami, a drugą jony przeciwnego znaku zgromadzone w roztworze na równoległej do powierzchni metalu płaszczyźnie oddzielone od fazy metalicznej cienką warstwą rozpuszczalnika. W takim ujęciu graniczące fazy jak i ładunki nie mają struktury ziarnistej lecz ciągłą. Model taki został stworzony przez F. Quincke’go w 1861 r. i H. Helmholtza w 1879 roku. Jeżeli przez D oznaczymy stałą dielektryczną rozpuszczalnika a przed d odległość "okładek" takiego kondensatora to całkowita pojemność elektryczna układu będzie równa:

Pojemność różniczkowa, czyli stosunek zmiany ładunku do wywołującej ją zmiany potencjału dana jest wzorem:

Znając zależność pojemności różniczkowej podwójnej warstwy elektrycznej od potencjału elektrody można obliczyć pojemność całkowitą elektrody przez całkowanie zmian gęstości ładunku odpowiadającej dowolnemu potencjałowi. Dane doświadczalne wykazały, że taki model daje rezultaty trudne do interpretacji; można go stosować jedynie do interpretacji wyników dla elektrod zanurzonych w dostatecznie stężonych roztworach elektrolitów. W modelu kondensatora płaskiego nie uwzględnia się ruchów cieplnych cząsteczek i jonów, które prowadzą do rozmycia w przestrzeni ładunków traktowanych w modelu jako zlokalizowane na płaszczyźnie w roztworze. 

Teorie uwzględniającą rozmyty charakter ładunków w podwójnej warstwie elektrycznej opracowali G. Gouy w 1910 r. i D. Chapman w 1913 r. Opracowując swoją teorię posłużyli się dwoma podstawowymi zależnościami:

(1) równaniem Poissona wiążącym gęstość ładunku w określonym punkcie przestrzeni w odległości "x" od punktu centralnego z umieszczonym w nim ładunkiem, z wartościami potencjału elektrycznego:

gdzie dla elektrolitu z-wartościowego: ρ = ze(n₊ + n_–) (e - ładunek elektronu, n - liczba jonów w 1 cm³ roztworu)

(2) rozkładem Maxwella-Boltzmanna dla jonów każdego rodzaju w ośrodku o znanym rozkładzie potencjału.

Jeżeli przez n_i0 oznaczymy stężenie jonów danego rodzaju w tym obszarze ośrodka w głębi roztworu, w którym poziom potencjału umownie przyjmujemy za równy zeru, to w obszarze o dowolnym potencjale panujące tam stężenie będzie dane zależnością:

W tej teorii, podobnie jak w opracowanej później teorii elektrolitów Hükela i Debye’a zasadniczą rolę odgrywa parametr "grubości" rozmytej warstwy jonowej 1/n. "Grubość" tę należy rozumieć w ten sposób, że jest to odległość, na której potencjał spada do e-tej części swej wartości przy samej powierzchni elektrody (e jest podstawą logarytmu naturalnego). W takim przypadku:

φ = φ₀exp(–χx), dla x = χ^–1, φ = φ₀e^–1

Pod względem oddziaływań elektrostatycznych model kondensatora płaskiego o odległości okładek χ^–1 jest równoważny układowi z omówionym rozmytym rozkładem ładunku przeciwjonów. Wartość tak pojętej grubości warstwy rozmytej jest odwrotnie proporcjonalna do pierwiastka kwadratowego stężenia 1-wartościowego roztworu elektrolitu w głębi roztworu, a w wprost proporcjonalna do pierwiastka ze stałej dielektrycznej i temperatury bezwzględnej ośrodka:

Teoria ta pozwoliła powiązać gęstość ładunku na powierzchni elektrody ze spadkiem potencjału φ₀ w podwójnej warstwie elektrycznej oraz stężeniem n₀ elektrolitu w roztworze:

O. Stern w 1924 roku uwzględnił możliwość zbliżania się pewnej ilości jonów na odległość nie mniejszą od określanej obecnie symbolem x₂ od powierzchni metalu. Jony te gromadzą się na okładce kondensatora płaskiego z modelu Helmholtza. tworząc tzw. część zwartą podwójnej warstwy elektrycznej. Pozostałe jony kompensujące ładunek powierzchniowy metalu znajdują się w części rozmytej opisanej w teorii Gouy’a i Chapmana.

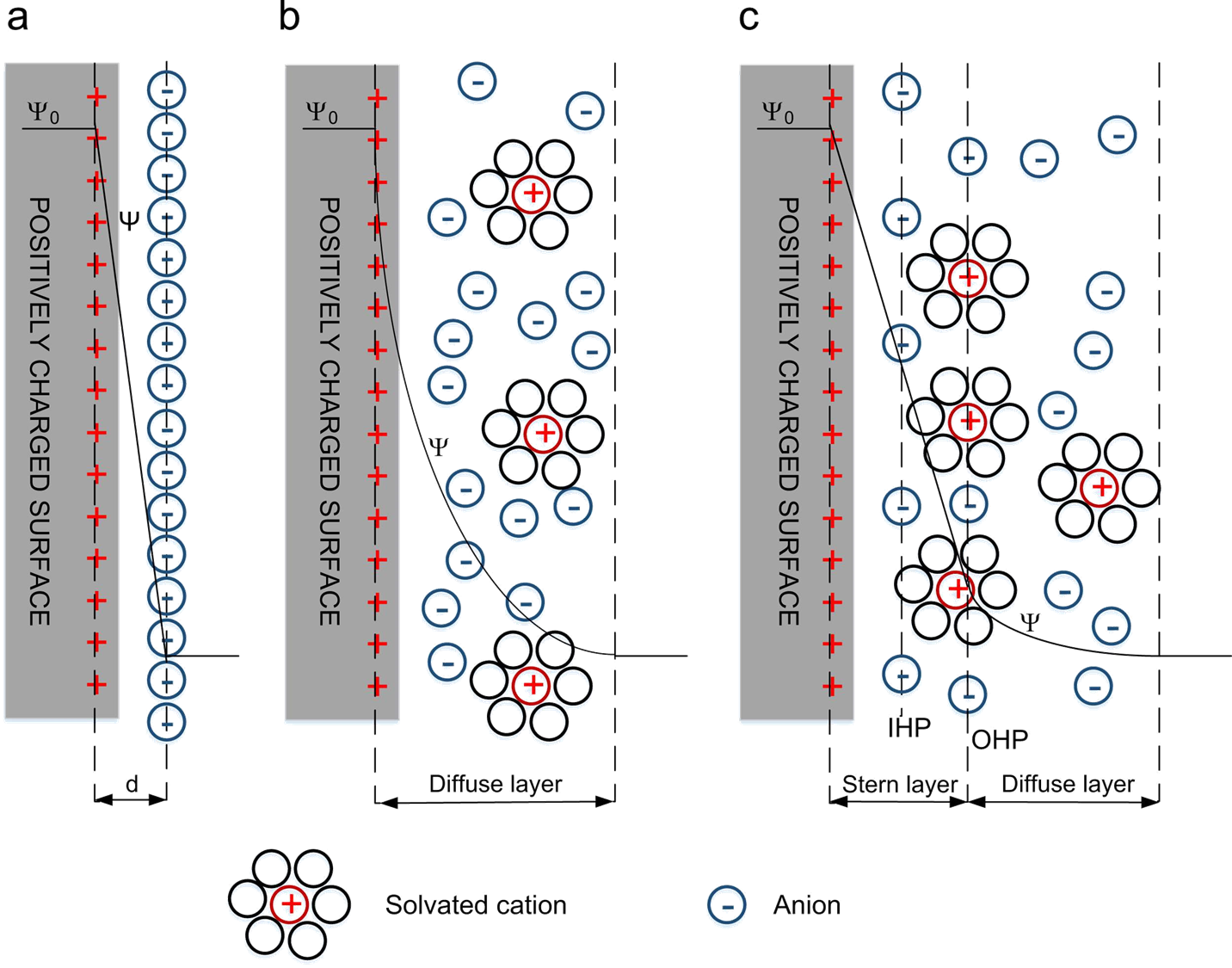Modele podwójnej warstwy elektrycznej: a) Helmholtza, b) Gouy’a-Chapmana, c) Sterna.

W 1947 roku D. C. Grahame zmodyfikował model Sterna dzieląc obszar warstwy podwójnej dwiema płaszczyznami równoległymi do powierzchni metalu.

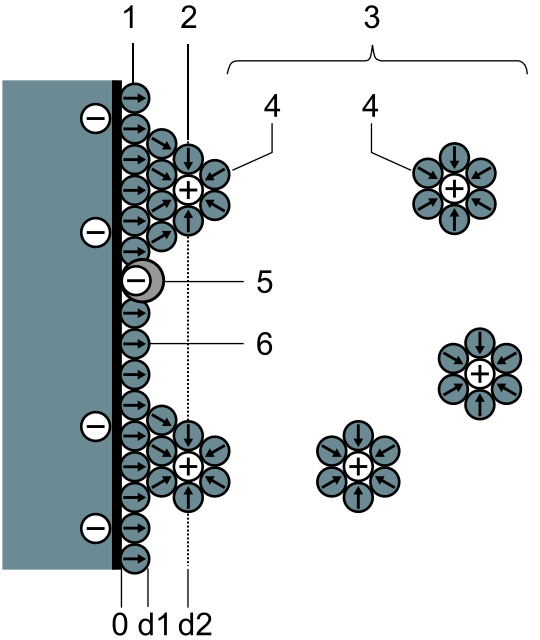Schemat modelu Grahame’a podwójnej warstwy elektrycznej 1. wewnętrzna płaszczyzna Helmholtza; 2. zewnętrzna płaszczyzna Helmholtza; 3. płaszczyzna dyfuzyjna; 4. solwatowane kationy; 5. specyficznie zaadsorbowane jony; 6. cząsteczki w roztworze elektrolitu.

Położenie zewnętrznej płaszczyzny Helmholtza wyznaczają na ogół środki ciężkości kationów, natomiast płaszczyznę wewnętrzną obsadzają środki ciężkości anionów w stanie ich najsilniejszego zbliżenia do powierzchni metalu. Od zewnętrznej płaszczyzny Helmholtza ku wnętrzu roztworu rozciąga się część rozmyta podwójnej warstwy elektrycznej. Aniony łatwiej od kationów mogą tracić swoją otoczkę hydratacyjną (w ogólności solwatacyjną) co uzasadnia ich większe zbliżanie się do powierzchni metalu niż w przypadku silnie solwatowanych kationów. Ponadto aniony znacznie częściej niż kationy ulegają specyficznej adsorpcji, wiążąc się nawet z ujemnie naładowaną powierzchnią metalu siłami nieelektrostatycznymi. Konsekwencją tej silnej specyficznej adsorpcji anionów jest zmiana potencjału zerowego ładunku elektrody towarzysząca zmianie stężenia elektrolitu. Uwzględnienie tego procesu pozwoliło na wyjaśnienie efektu Jesina-Markowa polegającego na przesuwaniu potencjału zerowego ładunku przy zmianie stężenia elektrolitu.

W wielu przypadkach gdy specyficzna adsorpcja jest słaba model Sterna daje dobre wyniki. Istota tego modelu sprowadza się do zastosowania izotermy Langmuira dla obliczenia stężenia jonów w części zwartej podwójnej warstwy elektrycznej.