Hybrydyzacja

Orbitale cząsteczkowe, w pierwszym przybliżeniu można skonstruować biorąc pod uwagę pary nakrywających się orbitali atomowych. Taki tok postepowania jest zasadą metody LCAO czyli metody posługującej się liniową kombinacja orbitali atomowych do tworzenia orbitali cząsteczkowych. Natomiast jak pokazały wyniki obliczeń, jeżeli energia orbitali atomowych jest zbliżona to w tworzeniu orbitalu cząsteczkowego biorą udział nie czyste orbitale atomowe, ale ich mieszaniny nazywane orbitalami zhybrydyzowanymi. Dla przykładu rozważmy cząsteczkę wodorku litu. Jako bazę do konstrukcji orbitali cząsteczkowych przyjęto zbiór orbitali 1s, 2s i 2p¹ litu oraz orbital 1s wodoru. Wyniki obliczeń pokazują, że orbital 1s litu pozostaje w cząsteczce jego wodorku praktycznie niezmieniony, natomiast w cząsteczce pojawia się wiążący orbital σ, który jest opisywany jako mieszanina orbitali atomowych o składzie: 0,323φ_2sLi + 0,231φ_2pLi + 0,685φ_H. Unormujmy współczynniki przy orbitalu zhybrydyzowanym litu w taki sposób aby orbital wiążący w cząsteczce był tworzony w wyniku nakładania jednego orbitalu atomu litu i wodoru. Ogólny warunek normowania ma w tym przypadku postać: ∫(aφ_2s+ bφ_2p)²dτ = a² + b² = 1. W wyniku przeprowadzenia matematycznych operacji otrzymuje wyrażenie: 0,397φ_hybr+ φ_H, opisujące orbital wiążący w cząsteczce LiH.

Hybrydyzacja orbitali powoduje zwiększenie wartości całki nakrywania, gdyż hybrydy są skierowane wzdłuż osi wiązania. Dodatkowym czynnikiem jest obniżenie energii hybrydy w stosunku do "czystych" orbitali atomowych tworzących wiązanie. Obniżenie energii jest ściśle związane ze wzrostem gęstości elektronowej w obszarze nakrywania czyli w obszarze wiązania. Natomiast nasuwa się pytanie czy istnieją jakieś czynniki, które przeciwdziałają hybrydyzacji, skoro proces ten wydaje się być korzystny ze względów energetycznych.

Pierwszym czynnikiem jest różnica w energii orbitali jakie ulegają hybrydyzacji. Akurat w rozważanym przypadku wodorku litu, różnica energii pomiędzy orbitalami 2s i 2p litu jest niewielka. Gdyby była ona większa wtedy udział orbitalu 2p w hybrydzie byłby znacznie mniejszy. Wynika o z prostego faktu, otóż wartość energii elektronu na orbitalu zhybrydyzowanym φ_hybr = aφ_2s+ bφ_2p wynosi: ε_hybr = a²ε_2s + b²ε_2p

Ponieważ a² + b² = 1 i obydwie zmienne są liczbami całkowitymi, to energia orbitalu zhybrydyzowanego jest średnią ważoną o wartości pomiędzy ε_2s i ε_2p. Obniżenie energii w wyniku utworzenia wiązania, któremu sprzyja zwiększenie współczynnika b (równego zero w przypadku orbitalu 2s), jest wyrównywane zwiększaniem się atomowej składowej energii związanej z elektronami obsadzającymi orbital zhybrydyzowany. Jeżeli energia ε_2p jest znacznie większa od ε_2s zmieszanie z orbitalem 2p wymaga znacznej energii i hybrydyzacja staje się niekorzystna energetycznie.

To co jest istotne, i o czym należy bezwzględnie pamiętać, to fakt, że hybrydyzacja nie jest zjawiskiem fizycznym. Stanowi ona jedynie element opisu teoretycznego.

Rozpatrując w dalszym ciągu cząsteczkę LiH, zauważmy, że po hybrydyzacji część gęstości elektronowej z orbitalu 2s znalazła się na orbitalu 2p. Z tego wynika, że gęstość prawdopodobieństwa znalezienia elektronu na orbitalu zhybrydyzowanym wynosi:

P_hybr = φ²_hybr =a²φ²_2s+ b²φ²_2p + 2abφ_2sφ_2p

Po scałkowaniu tego równania otrzymujemy wartość 1 odpowiadającą jednemu elektronowi. Trzeci wyraz w równaniu daje wartość zero z tego względu, że orbitale 2s i 2p są ortogonalne. Natomiast człon ten odpowiada za polaryzację gęstości P_hybr powodując, że jest ona przesunięta w kierunku dodatniego płata orbitalu p. Teraz konfigurację atomu litu w cząsteczce LiH możemy zapisać w postaci Li[1s²2p^0,6612p^0,339], co odpowiada przeniesieniu 0,339 elektronu z orbitalu 2s na orbital 2p. Taki zapis konfiguracji elektronowej nosi nazwę stanu walencyjnego.. Populacja elektronowa orbitali zhybrydyzowanych ma znaczenie gdy w wyniku tego procesu powstają dwa, lub więcej, orbitali hybrydowych. Z jednego orbitalu s i jednego p możemy utworzyć dwa orbitale typu sp. Teraz jeżeli jeden z nich ma populację odpowiednio 30% s i 70% p to drugi będzie składał się z 70% p i 30% s.

Hybrydyzacja jest mniej kosztowna energetycznie jeżeli różnica ε_2s – ε_2p jest mała, co ma miejsce w przypadku gdy liczba elektronów walencyjnych jest niewielka. W związku z tym należy jej się spodziewać w przypadku pierwiastków znajdujących się po lewej stronie układu okresowego. Jest to szczególnie widoczne dla dwuatomowych cząsteczek heterojądrowych jak cząsteczka tlenku węgla CO. Nie uwzględniając hybrydyzacji orbitali s i p węgla diagram orbitali cząsteczkowych dla CO ma następującą postać:

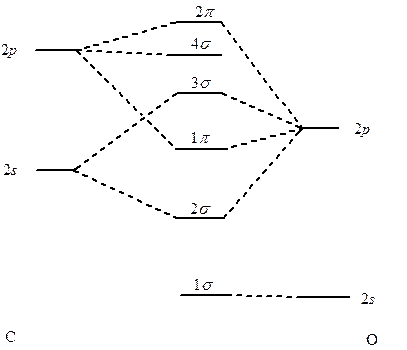Korelacyjny diagram orbitali cząsteczkowych cząsteczki tlenku węgla bez uwzględnienia hybrydyzacjiTaki obraz budowy cząsteczki CO jest niezgodny z doświadczeniem. Na diagramie znajduje się jedna para elektronowa na orbitalu 1σ należącym do tlenu i antywiążąca para elektronowa zajmująca orbital 3σ. Natomiast jeżeli uwzględni się pewien, niewielki, udział zmieszania orbitali 2s i 2p atomu węgla oraz tlenu to na diagramie korelacyjnym pojawia się orbital 3σ będący głównie orbitalem 2p węgla, z niewielką domieszką 2s, zawierającym wolną parę elektronową. Dodatkowo cechą tego orbitalu jest to, że jest on zwrócony w stronę przeciwną niż wiązanie węgiel–tlen. taki stan odpowiada właściwościom cząsteczki CO, która jest bardzo dobrym ligandem koordynującym do atomów metali właśnie poprzez atom węgla, wykorzystując parę elektronową zlokalizowaną na orbitalu 3σ.

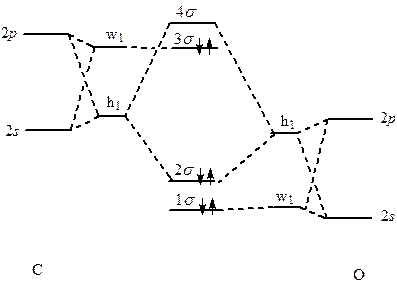Diagram korelacyjny dla cząsteczki CO uwzględniający hybrydyzację. Uwzględnienie hybrydyzacji orbitali przy tworzeniu wiązania chemicznego wskazuje na lokalizacje rozkładu ładunku tworzącego wiązanie. Inaczej mówiąc o ile teoria orbitali cząsteczkowych posługuje się orbitalami niezlokalizowanymi, obejmującymi całą cząsteczkę, to jednak wyniki czy to badań spektroskopowych czy ciepeł tworzenia związków chemicznych wskazują na lokalizację wiązań. Inaczej mówiąc każde oddzielne wiązanie w cząsteczce wieloatomowej przypomina typowe dwucentrowe wiązania chemiczne, czyli że elektrony wiążące są na ogół zlokalizowane w obszarze jednego poszczególnego wiązania. Jednocześnie takie podejście ma jeszcze jedną cechę. Otóż orbitale zlokalizowane łatwiej sobie wyobrazić gdyż zachowane jest w tej koncepcji pojęcie wiązania między dwoma atomami cząsteczki wieloatomowej. Oczywistym jest, że teoria zlokalizowanych wiązań całkowicie zawodzi w odniesieniu do związków, w których występują sprzężone układy wiązań wielokrotnych, lub też w przypadkach gdy wiązania w cząsteczce są obejmują więcej niż dwa centra jak na przykład w borowodorach.

Przykładem lokalizacji wiązań może być cząsteczka wody, której budowę rozpatrzymy pod kątem maksymalnego nakrywania orbitali atomowych tlenu i wodoru.

Rozmieśćmy atomy wodoru tak jak pokazano to na powyższym rysunku, czyli wzdłuż kierunków orbitali p atomu tlenu. W ten sposób zapewniamy maksymalne nakładanie orbitali s wodoru i p tlenu. W ten sposób do opisu wiązań w cząsteczce H₂O zamiast kombinacji wszystkich czterech orbitali używamy tylko po dwa na raz. W wyniku kombinacji powstają dwa zlokalizowane orbitale b₁ i b₂. Następna konsekwencją takiego podejścia, czyli zlokalizowania orbitali jest to, że zastępując jeden z atomów wodoru inna grupą spodziewamy się jedynie modyfikacji jednego orbitalu, b₁lub b₂, ponieważ elektrony wiązania O–H mają charakterystyczne funkcje falowe, co jest podstawą przybliżonej wartości energii, długości i innych cech wiązania.

Przybliżona niezależność dwóch wiązań O–H jest związana z brakiem nakrywania się orbitali atomowych użytych do ich opisu. Nakrywanie orbitali s wodoru można pominąć gdyż są one rozdzielone. Nakrywanie się orbitali p_x i p_y daje efekt zerowy ze względu na ich ortogonalność i wynika też z ich symetrii. Natomiast gdybyśmy użyli dwóch dowolnych orbitali p, pomiędzy którymi kąt nie wynosiłby 90° a miałby inna wartość wtedy całka nakrywania nie byłaby zerowa. Powstaje więc pytanie jaki jest powód takiego a nie innego opisu cząsteczki H₂O i dlaczego orbitale zlokalizowane są ortogonalne (całka nakrywania wynosi 0). Opis uwzględniający orbitale zlokalizowane jest wygodny, gdyż przy jego zastosowaniu mamy możliwość przedstawienia energii cząsteczki i jej kształtu jako zależnych od jej oddzielnych fragmentów, oraz energii ich wzajemnego oddziaływania. Innymi słowy separowalność wiązań w takim sensie, że każde z nich wnosi swój własny addytywny wkład do pełnej chmury ładunku w cząsteczce pozwala na opis rozkładu ładunku w postaci prostej sumy gęstości pochodzących od poszczególnych części cząsteczki. Zastosowanie do takiego opisu nieortogonalnych orbitali, choc jest możliwe, to jednak prowadzi do niezwykle skomplikowanych obliczeń matematycznych, w których gubi się tak poglądowość jak i sens fizyczny czynników, od których zależy energia cząsteczki.

Zastosujmy teraz hybrydyzację do opisu cząsteczki H₂O. Dopuszczając zmieszanie orbitali s, p_x, p_y i p_z otrzymujemy w efekcie cztery hybrydy zwrócone w różnych kierunkach. Dla cząsteczki wody użyjmy tylko orbitali p_x i p_y nakrywających się z atomami wodoru. Otrzymujemy w wyniku tego dwie hybrydy w postaci: s + λp_x oraz s + λp_y. Jednak tak skonstruowane hybrydy mają różną od zera całkę nakrywania, co uniemożliwia utworzenie z nich orbitali zlokalizowanych. W związku z tym tworzymy dwa orbitale zhybrydyzowane, jeden w kierunku orbitalu atomowego p₁ a drugi w kierunku orbitalu atomowego p₂. Możemy je przedstawić w postaci: h₁=N₁(s + λp₁) i h₂=N₂(s + λp₂). Zakładamy, że orbitale h₁ i h₂ są unormowane, a wtedy całka ich nakrywania ma postać:

∫h₁h₂dτ = N₁N₂[1+ λ₁∫sp₁dτ + λ₂∫sp₂xdτ + λ₁λ₂∫p₁p₂dτ]

Ponieważ pierwsze dwie całki znikają, pozostaje do wyznaczenia jedynie całka reprezentująca nakrywanie się dwóch dowolnie skierowanych orbitali typu p. Ponieważ orbital p₁ leży na osi x, to pamiętając o wektorowym charakterze funkcji typu p rozłóżmy p₂ na składowe:

p₂ = p_xcosθ₁₂ + p_ycsinθ₁₂.

 Zatem całka nakrywania jest równa:

∫p₁p₂dτ = cosθ₁₂∫p_x²dτ + sinθ₁₂∫p_xp_ydτ = cosθ₁₂

Zatem warunek ortogonalności wyraża się równaniem λ₁λ₂ = –1/cosθ₁₂. W takim wypadku kąt pomiędzy hybrydami zależy od względnych udziałów składników p₁ i p₂. Ponieważ λ₁ i λ₂ są dodatnie, a cosθ₁₂ jest ujemny to hybrydy muszą tworzyć kąt większy od 90°.

Wracając do cząsteczki wody i zakładając, że λ₁=λ₂, widzimy, że cosθ₁₂= –1/λ². Teraz podstawiając za θ₁₂ wartość eksperymentalną kąta równą 104,5° otrzymujemy λ=1,998. Wiedząc, że udziały orbitali s i p w hybrydzie wynoszą odpowiednio N² i N²/λ², możemy określić udział orbitalu p na 80% i s na 20%. Pozostaje jeszcze kwestia trzeciego orbitalu typu p atomu tlenu. Do utworzenia wiązań użyte zostały dwie hybrydy h₁ i h₂. Trzecia hybryda typu s + λp₃ ma kierunek ustalony przez warunek ortogonalności do h₁ i h₂. Orbital ten, na którym znajduje się wolna para elektronowa, leży na dwusiecznej kąta H–O–H, czyli wartości θ₁₃ i θ₂₃ wynoszą 127,65°. W efekcie orbital ten składa się z 60% z orbitalu s i 40% orbitalu p. Łączna zawartość orbitalu s we wszystkich hybrydach wynosi 2•0,20 + 0,60 = 1 (użyliśmy jednego orbitalu s), a orbitalu p jest równa 2•0,80 + 0,40 = 2, gdyż użyliśmy dwóch orbitali typu p.