 Principles of Chemistry
Principles of Chemistry
- > Home
-
>
Historia chemii
- > Początki chemii
- > Rozwój alchemii
- > Jatrochemia
- > Badanie spalania i powietrza
- > Odkrycie i badanie gazów
- > Powstanie nowoczesnej chemii
- > Prawa chemiczne
- > Narodziny teorii atomowej
- > Elektrochemia
- > Berzelius, Hisinger, Faraday
- > Początki chemii organicznej
- > Substytucja
- > Wartościowość
- > Chemia fizyczna
- > Rozwój chemii nieorganicznej
- > Struktura atomu
-
>
Pierwiastki
- > Starożytność
- > Średniowiecze
- > Powietrze i woda
- > Analiza chemiczna
- > Halogeny
- > Elektrochemia
- > Metody spektroskopowe
- > Pierwiastki ziem rzadkich
- > Gazy szlachetne
- > Pierwiastki radioaktywne
- > Szeregi pierwiastków promieniotwórczych
- > Pierwiastki otrzymane sztucznie
- > Pierwiastki transuranowe
- > Podsumowanie
- > Układ okresowy
-
>
Mechanika falowa
- > Podstawy teoretyczne
- > Moment pędu
- > Równanie Schrodingera
- > Oscylator liniowy
- > Pole o symetrii sferycznej i pole kulombowskie
- > Spin
- > Identyczność cząstek
- > Oddziaływanie wymienne
- > Druga kwantyzacja
- > Poziomy energetyczne atomów
- > Układ okresowy
- > Atom w polu elektrycznym
- > Atom w polu magnetycznym
- > Cząsteczka dwuatomowa
- > Orto- i parawodór
- > Teoria relatywistyczna
- > Kwantowanie pola elektromagnetycznego
- > Fotony
- > Równanie Diraca
- > Cząstki i antycząstki
- > Atom i cząsteczka
-
>
Związki metali przejściowych
- > Powłoka walencyjna metali przejściowych
- > Efekt Jahna-Tellera
- > Teoria pola krystalicznego
- > Teoria pola ligandów
- > Widma elektronowe
- > Wiązania metal-metal
- > Własności magnetyczne
- > Trwałość związków koordynacyjnych
- > Związki z ligandami π–akceptorowymi
- > Arenowe związki koordynacyjne
- > Oddziaływania agostyczne
- > Wiązania chemiczne
- > Pojęcia chemii nieorganicznej
- > Mechanizmy reakcji
- > Oddziaływania międzycząsteczkowe
- > Elementy fizyki
- > Chemia organiczna
Stany skupienia materii
Właściwości substancji zależą nie tylko od ich natury chemicznej ale również od stanu skupienia.
Gazy
Gazy ze względu na stosunkowo małe przyciąganie międzycząsteczkowe stosunkowo najłatwiej jest opracować pod względem teoretycznym. Objętość dowolnej substancji jest to przestrzeń jaką ona zajmuje. W przypadku gazów objętość próbki jest taka sama jak objętość zbiornika w jakim gaz się znajduje. W przypadku cieczy i ciał stałych objętość nie zmienia się znacznie wraz ze zmianami ciśnienia i temperatury. Dla gazów sytuacja jest inna. Z tego powodu aby ustalić liczbę moli w danej próbce gazu konieczne jest podanie ciśnienia, temperatury i objętości zajmowanej przez ten gaz. Po zmieszaniu ze sobą cieczy lub ciał stałych objętość mieszaniny jest w przybliżeniu równa sumie objętości składników. W przypadku gazów takie założenie nie jest słuszne, gdyż objętość mieszaniny zależy w głównej mierze od ciśnienia końcowego. Wynika to z faktu, że wszystkie gazy można mieszać ze sobą w dowolnych stosunkach.
Temperatura
Powszechnie znane jest zjawisko przepływu temperatury od ciała cieplejszego do zimniejszego. Tłumaczy się to przepływem energii cieplnej od ciała gorącego do zimnego. W związku z tym temperaturę określa kierunek przepływu ciepła. Skalą temperatur jest obecnie skala bezwzględna, w której zero bezwzględne jest najniższą temperaturą od której niższej nie da się uzyskać. Skala ta nosi nazwę skali Kelvina, który zaproponował jej stosowanie w roku 1848, i którą definiuje się prze odniesienie do wartości 273,16K do temperatury, w której woda współistnieje we wszystkich trzech stanach skupienia. Wartość ta odpowiada punktowi, w którym woda w stanie ciekłym, stałym i gazowym współistnieje w równowadze, Inaczej mówiąc temperatura kelwina jest określana jako 1/273,16 różnicy temperatur pomiędzy zerem bezwzględnym a punktem potrójnym wody. W skali Kelwina temperatura krzepnięcia wody wynosi 273,15°C. Liczbę 273 wybrano na podstawie doświadczeń, zgodnie z którymi w warunkach doskonałych wszystkie gazy rozszerzają się jednakowo wraz ze wzrostem temperatury. W temperaturze 0°C przyrost objętości zawsze wynosi 1/273 badanej objętości. potrójny punkt wody jest o 0,01° wyższy od normalnej temperatury krzepnięcia wody w skali Kelvina, czyli temperatura krzepnięcia wody wynosi 273,15K. Normalna temperatura krzepnięcia wody jest ustalona jako punkt zerowy w skali Celsiusa, oznaczony jako 0°C. Normalna temperatura krzepnięcia wody jest ustalona jako punkt zerowy w skali Celsjusza i jest ona taka sama jak w skali Kelvina. Temperatura wrzenia wody pod normalnym ciśnieniem w skali Celsjusza wynosi 100°, co jest taką samą wartością jak w skali Kelvina. Natomiast stopień w obydwu skalach odpowiada jedynie 5/9 stopnia w skali Fahrenheita . Temperaturę w skali Celsjusza przelicza się na Kelwiny dodając 273,15, natomiast w skali Fahrenheita trzeba uwzględnić poprawkę:
(°F –32)5/9 +273,15 = temperatura w skali Kelvina
Ciśnienie
Określa kierunek przepływu masy. Substancje starają się poruszać z miejsca, w którym panuje wyższe ciśnienie do miejsca gdzie ciśnienie jest niższe. Ilościowo ciśnienie definiuje się jako siłę wywieraną prostopadle na jednostkę powierzchni. Podstawową jednostką ciśnienia jest paskal, czyli N/m2. W płynach (gaz i ciecze) ciśnienie jest w danym punkcie jest jednakowe we wszystkich kierunkach.
Prawo Boyle’a
Charakterystyczną właściwością gazów jest ich duża ściśliwość. Ilościowo zachowanie takie opisuje prawo Boyle’a, zgodnie z którym w stałej temperaturze określona objętość gazu zajmuje objętość odwrotnie proporcjonalną do ciśnienia pod jakim się znajduje. Formalnie prawo to przyjmuje postać:
P·V = const lub V = const/P
Wielkość stałej w tych równaniach określa masa próbki i jej temperatura. Dla gazów rzeczywistych prawo to jest spełnione pod niewielkimi ciśnieniami i przy wysokich temperaturach. Gdy temperatura spada, lub też wzrasta ciśnienie obserwuje się odstępstwa od tego prawa. Na podstawie odchyleń od prawa Boyle’a holenderski uczony J. D. van der Waals zaproponował skorygowaną wersję zależności ciśnienia i objętości gazu:
![]()
gdzie:
a – stała charakterystyczna dla danego gazu, uwzględniająca oddziaływanie między cząsteczkami gazu (cząsteczki gazu przyciągają się, w wyniku czego rzeczywiste ciśnienie gazu na ścianki naczynia jest mniejsze niż w przypadku, gdyby tego oddziaływania nie było),
b – stała charakterystyczna dla danego gazu, uwzględniająca skończone rozmiary cząsteczek, ma wymiar objętości, przez co uznawana jest za objętość mola cząsteczek gazu,
p – ciśnienie,
Vm = V/n – objętość molowa,
V – objętość,
n – liczność materii. liczba moli,
T – temperatura bezwzględna,
R – uniwersalna stała gazowa.
Dla dowolnej liczby moli gazu n w objętości V równanie van der Waalsa przybiera postać:
![]()
Parametry a i b są związane z parametrami punktu krytycznego gazu, czyli temperaturą i ciśnieniem powyżej których nie można skroplić gazu.
Prawo Charlesa
Inną charakterystyczną właściwością gazów jest rozszerzanie się pod wpływem ciepła. Zależność ciśnienia od temperatury określa prawo Charlesa, zwane również prawem Gay-Lussaca. Zgodnie z tym prawem ciśnienie gazu p w stałej objętości zwiększa się o stały ułamek ciśnienia tego gazu zmierzonego w temperaturze 0 °C przy wzroście temperatury o 1 °C.
![]()
p – ciśnienie gazu,
p0 – ciśnienie gazu w temperaturze 0 °C,
T – temperatura bezwzględna,
t [°C] = T [K] – 273,15 – temperatura w skali Celsjusza.
Prawo Daltona
To ogólne stwierdzenie obejmuje dwa, wzajemnie komplementarne, prawa gazowe sformułowane przez Johna Daltona. Pierwsze z nich to prawo ciśnień cząstkowych, zgodnie z którym ciśnienie wywierane przez mieszaninę gazów jest równe sumie ciśnień wywieranych przez składniki mieszaniny, gdyby każdy z nich był umieszczany osobno w tych samych warunkach objętości i temperatury, jest ono zatem sumą ciśnień cząstkowych. Można to przedstawić w formie matematycznej w postaci:

gdzie:
p – ciśnienie w mieszaninie k-składnikowej w objętości V i temperaturze T
pi – ciśnienie cząstkowe składnika i w tej samej objętości i temperaturze
Drugie to prawo objętości cząstkowych, które głosi, że objętość zajmowana przez mieszaninę gazów jest równa sumie objętości, które byłyby zajmowane przez składniki mieszaniny, gdyby każdy z nich był umieszczony osobno w tych samych warunkach ciśnienia i temperatury, czyli jest równa sumie objętości cząstkowych.

gdzie:
V – objętość mieszaniny k-składnikowej przy ciśnieniu p i temperaturze T
Vi – objętość cząstkowa składnika i w tej samej temperaturze i ciśnieniu.
Zasada Avogadra
Prawo Avogadra brzmi: W tych samych warunkach fizycznych tj. w takiej samej temperaturze i pod takim samym ciśnieniem, w równych objętościach różnych gazów znajduje się taka sama liczba cząsteczek. W warunkach normalnych jeden mol gazu doskonałego zajmuje objętość 22,415 dm³ (jest to jego objętość molowa). Dla gazów rzeczywistych objętość ta nieco się różni. Prawo Avogadra jest prawem przybliżonym, którego zakres stosowalności zależy od podobieństwa porównywanych gazów rzeczywistych do gazu doskonałego.
Równanie stanu
Prawo Boyle’a, Charlesa-Gay-Lussaca i Zasadę Avogadra można połączyć otrzymując ogólną zależność pomiędzy objętością, ciśnieniem, temperaturą i liczbą moli w próbce gazu. Taka ogólna zależność nosi nazwę równania stanu, które określa w jaki sposób przy przejściu z jednego stanu gazowego w inny zmieniają się parametry V, P, T i n. Prawo Boyle’a, Charlesa-Gay-Lussaca i zasadę Avogadra można zapisać w takiej postaci:
V ~ 1/P przy stałych T i n<
V ~ T przy stałych p i n
V ~ n przy stałych T i P
lub ogólnie:
V ~ 1/P Tn
Zamiast proporcjonalności można zapisać równanie:
PV = nRT
gdzie stała proporcjonalności R oznacza uniwersalną stałą gazową. Wartość liczbową R można łatwo wyznaczyć podstawiając do wzoru parametry warunków normalnych czyli T=273,5 K, P=101325 Pa, n=1 (1 mol gazu) i V=22,414·10–3 m3. Otrzymujemy wtedy wartość R = 8,3143 J/K·mol. Uwzględnienie oddziaływań pomiędzy cząsteczkami gazu prowadzi do przedstawionego powyżej równania van der Waalsa.
Prawo dyfuzji Grahama
Gaz rozprzestrzenia się w taki sposób, że zajmuje całą dostępną mu przestrzeń. Taki samorzutny proces nosi nazwę dyfuzji. Szybkość dyfuzji gazów jest związana z ich gęstością i określa ją prawo Grahama, zgodnie z którym: Szybkość dyfuzji gazów jest odwrotnie proporcjonalna do pierwiastka kwadratowego z ich gęstości. Matematycznie można to przedstawić w formie:
![]()
gdzie:
v – szybkość efuzji gazu,
ρ – gęstość gazu.
W przypadku porównywania dyfuzji dwóch gazów będących w tej samej temperaturze i pod takim samym ciśnieniem możemy skorzystać z zależności:
![]()
gdzie indeksy 1 i 2 oznaczają odpowiednie gazy. Generalnie gazy cięższe dyfundują wolniej niż lżejsze.
Ciecze
Ciecze są praktycznie nieściśliwe, więc inaczej niż w gazach, zmiany ciśnienia nie powodują praktycznie większych zmian objętości. Teoria wyjaśnia to zjawisko zakładając, że przestrzeń pomiędzy cząsteczkami cieczy jest bardzo mała. Ciecze zachowują swoją objętość niezależnie od kształtu i wielkości pojemnika. Dyfuzja w cieczach zachodzi powoli, co wynika z faktu, że w cieczy cząsteczki nie mogą poruszać się swobodnie na duże odległości z powodu zderzeń z sąsiednimi cząstkami.

Ciśnienie pary nasyconej
Jeżeli ciecz znajduje się w zamkniętym pojemniku to w układzie po pewnym czasie ustala się dynamiczna równowaga pomiędzy parowaniem i skraplaniem. Cząsteczki w stanie pary wywierają pewne ciśnienie, które jest charakterystyczne dla danej cieczy. Wartość ciśnienia pary nasyconej zależy od rodzaju cieczy i od temperatury. Zależność od rodzaju cieczy wynika z tego, że każda ciecz odznacza się charakterystyczną wielkością sił przyciągania pomiędzy cząsteczkami. Natomiast w miarę wzrostu temperatury cieczy średnia energia kinetyczna cząsteczek wzrasta, co powoduje, że wzrasta liczba cząsteczek o energii dostatecznej do przejścia w stan pary, a tym samym wzrasta ciśnienie pary nasyconej. Zależność pomiędzy ciśnieniem pary nasyconej i temperaturą opisuje równanie Clausiusa-Clapeyrona:

gdzie P – ciśnienie pary nasycone; T – temperatura; ΔH’ ciepło potrzebne do przemiany 1 mol cieczy w stan gazowy.
Mierząc ciśnienie pary nasyconej w dwóch różnych temperaturach można wykorzystują powyższe równanie ocenić wartość ΔH’. Odwrotnie jeżeli znana jest wartość ΔH’ to ciśnienie pary w jednej temperaturze można obliczyć na podstawie ciśnienia zmierzonego w innej temperaturze.
Temperatura wrzenia, napięcie powierzchniowe i lepkość
Wrzenie jest szczególnym przypadkiem parowania. Ciecz wrze w temperaturze odpowiadającej punktowi wrzenia, czyli temperaturze w której ciśnienie pary cieczy zrówna się z ciśnieniem zewnętrznym. W temperaturze wrzenia ciśnienie pary jest dostatecznie wysokie aby przeciwdziałać ciśnieniu atmosferycznemu i umożliwić tworzenie się pęcherzyków pary w całej objętości cieczy. Ponieważ każda ilość ciepła dostarczona cieczy w temperaturze wrzenia jest zużywana na dostarczenie cząsteczkom energii potrzebnej do wyparowania to średnia energia cząsteczek pozostających w cieczy nie wzrasta. W związku z tym temperatura wrzenia czystej cieczy pozostaje stała.
Napięcie powierzchniowe odnosi się do siły wewnątrz cieczy, która działa równolegle do powierzchni i wykazuje skłonność do jej rozciągania. Siła ta wynika z przyciągania międzycząsteczkowego. Siły napięcia powierzchniowego wpływają na kształt swobodnej (niestykającej się ze ściankami naczynia) powierzchni cieczy, przy czym na ogół współistnieją przy tym z innymi siłami. Współistnienie sił napięcia powierzchniowego, sił przylegania oraz grawitacji prowadzi do powstawania menisku: powierzchnia cieczy w sąsiedztwie ścianki zbiornika 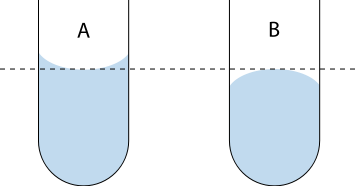 Menisk w kapilarze A – wklęsły, B – wypukły.
Menisk w kapilarze A – wklęsły, B – wypukły.
Lepkość jest właściwością cieczy charakteryzującą ich tarcie wewnętrzne wynikające z przesuwania się względem siebie warstw płynu podczas przepływu. Zgodnie z laminarnym modelem przepływu (płyn przepływa warstwami bez zaburzeń) lepkość wynika ze zdolności płynu do przekazywania pędu pomiędzy warstwami poruszającymi się z różnymi prędkościami. Model laminarny lepkości zawodzi też przy przepływie turbulentnym, powstającym np. na granicy płynu i ścianek naczynia. Dla przepływu turbulentnego jak dotąd nie istnieją dobre modele teoretyczne.
Ciało stałe
O ile gazy charakteryzują się nieuporządkowaniem, o tyle ciała stałe charakteryzuje porządek, w którym atomy są rozmieszczone według określonego modelu. Ciało stałe, w przeciwieństwie do gazów i cieczy zajmuje charakterystyczną objętość, która nie zmienia się ani ze zmiana naczynia ani z niezbyt wielkimi zmianami ciśnienia i temperatury. Dyfuzja w ciałach stałych zachodzi bardzo powoli. Ciała stałe tworzą kryształy o określonych postaciach geometrycznych charakterystycznych dla poszczególnych substancji. Nie wszystkie ciała stałe mają postać krystaliczną. Niektóre substancje stałe, jak szkła, mają właściwości stanu stałego ale nie posiadają uporządkowanego stanu krystalicznego. Substancje takie noszą nazwę amorficznych ciał stałych.
Informacje o ułożeniu podstawowych cząstek w ciele stałym można uzyskać stosując dyfrakcję promieni rentgenowskich. Dyfrakcja promieni X jest procesem złożonym wywołującym wzajemne oddziaływanie pomiędzy promieniowaniem i elektronami w atomach. Dla kryształu składającego się z wielu atomów lub cząsteczek ułożonych regularnie występują pewne kąty względem padającej wiązki promieniowania rentgenowskiego, pod którymi następuje wzmocnienie wiązki. Zależność pomiędzy katami wiązki padającej a odległościami międzypłaszczyznowymi sieci krystalicznej podaje prawo Braggów:
nλ = 2dsinΘ
gdzie n – liczba całkowita; λ – długość fali promieniowania rentgenowskiego; d – odległość międzypłaszczyznowa atomów tworzących rozpatrywane zakłócenie wzdłuż kierunku, który tworzy kąt 2Θ z kierunkiem padającej wiązki. Staranna analiza matematyczna obrazu dyfrakcyjnego umożliwia obliczenie najbardziej prawdopodobnego położenia cząstek w badanym układzie. Układ punktów określający położenie cząstek lub atomów w krysztale nosi nazwę sieci przestrzennej. Sieć krystaliczna charakteryzuje się uporządkowaniem dalekiego zasięgu oraz symetrią. Najmniejszą, powtarzalną składową sieci krystalicznej jest komórka elementarna. Najmniejszym, powtarzającym się periodycznie w przestrzeni fragmentem sieci przestrzennej jest równoległościan nazywany komórką elementarną. Krawędzie komórki wyznaczają osie układu odniesienia, które określane są osiami krystalograficznymi. Rozmiary i kształt komórki elementarnej są określone przez stałe sieciowe, którymi są periody identyczności (a, b, c) oraz kąty pomiędzy osiami (α, β, γ). Sieć przestrzenna jest jednoznacznie określona przez jej komórkę elementarną. Własności symetrii sieci krystalicznej zawierają się w grupach przestrzennych. Kryształy klasyfikuje się ze względu na układ wewnętrzny cząsteczek w sieci krystalicznej. Układ krystalograficzny definiuje się także jako zespół klas symetrii, których elementy powodują jednakowe ograniczenia stałych sieciowych komórki elementarnej sieci przestrzennej. System wyróżnia siedem układów, w których wyróżnia się 32 klasy krystalograficzne.
| Układ | Jednostki osiowe | Kąty między osiami |
| regularny | a = b = c | α = β = γ = 90° |
| tetragonalny | a = b ≠ c | α = β = γ = 90° |
| rombowy | a ≠ b ≠ c | α = β = γ = 90° |
| jednoskośny | a ≠ b ≠ c ≠ a | α = γ = 90°; β ≠ 90° |
| trójskośny | a ≠ b ≠ c ≠ a α ≠ β ≠ γ ≠ α |
α, β, γ ≠ 90° |
| heksagonalny | a = b ≠ c | α = β = 90°; γ = 120° |
| trygonalny (romboedryczny) |
a = b ≠ c (a = b = c) |
α = β = 90°; γ = 120° (α = β = γ ≠ 90°) |
Defekty sieci
 Dyslokacje krawędziowa i śrubowa
Dyslokacje krawędziowa i śrubowa
Zazwyczaj zdefektowanie sieci rośnie wraz ze wzrostem temperatury. Defekty sieci krystalicznej odpowiadają za różne właściwości kryształów, między innymi półprzewodnictwo typu n lub p, barwę, luminescencję.
Wiązania w ciałach stałych
Często zamiast klasyfikowania ciał stałych na podstawie symetrii uporządkowania lub upakowania atomów w sieci krystalicznej celowe jest ich klasyfikowanie według rodzaju cząstek jakie zajmują węzły sieci i sposobu ich wiązania. Kryształy sklasyfikowane są w czterech grupach.
| Cząsteczkowe | Jonowe | Atomowe | Metaliczne | |
| Cząstki zajmujące węzły sieci | cząsteczki | jony (kationy i aniony) | atomy | jony dodatnie w gazie elektronowym |
| Siła wiążąca |
van der Waalsa dipol-dipol |
przyciąganie elektrostatyczne | wspólne pary elektronowe | przyciąganie elektrostatyczne pomiędzy jonami i elektronami |
| Własności | bardzo miękkie; niska temperatura topnienia; lotne; dobre izolatory | twarde i kruche; stosunkowo wysoka temperatura topnienia; dobre izolatory | bardzo twarde; bardzo wysoka temperatura topnienia; izolatory | twarde lub miękkie; średnia do bardzo wysokiej temperatura topnienia; dobre przewodniki |
| Przykłady | H2; H2O; CO2 | NaCl; KBr; NaNO3 | diament; SiO2; SiC | Na; Cu; Fe |
Wielkość sił przyciągania w kryształach można mierzyć energią spójności kryształu, która jest ilością energii potrzebną do przemiany 1 mola substancji ze stanu stałego do stanu gazowego, w którym cząstki gazowe są takie same jak jednostki zajmujące miejsce w sieci krystalicznej. W przypadku ciała stałego cząsteczkowego energia spójności odpowiada energii sublimacji, czyli energii potrzebnej do wytworzenia 1 mola gazu cząsteczkowego. W przypadku jonowych ciał stałych jest to energia potrzebna do wytworzenia jonów dodatnich i ujemnych w postaci gazu z jednego mola ciała stałego. W kryształach kowalencyjnych jest to energia niezbędna do wytworzenia gazu atomowego. Natomiast w przypadku metali węzły sieci zajmują jony a stan końcowy obojętne atomy.
Krzywe ogrzewania i chłodzenia

Krzywą chłodzenia otrzymuje się gdy energię cieplną odprowadza się od substancji ze stałą szybkością. W początkowym etapie tego procesu średnia energia kinetyczna gazu zmniejsza się i tym samym temperatura ulega obniżeniu. Energia kinetyczna gazu zmniejsza się do momentu gdy siły przyciągania pomiędzy cząstkami nie zaczną przeważać i gaz ulega skropleniu. Ponieważ przejście cząstki z cieczy do gazu zużywa energię to w procesie odwrotnym energia jest wydzielana. To zmniejszenie energii potencjalnej podczas skraplania dostarcza energii cieplnej kompensujące jej ubytek z układu i temperatura podczas skraplania pozostaje stała. Gdy wszystkie cząstki uległy kondensacji i w układzie znajduje się tylko ciecz dalsze odprowadzanie energii powoduje obniżanie temperatury do momentu gdy nie rozpocznie się proces zestalania. Podczas krystalizacji cząstki zajmują określone pozycje w sieci przestrzennej co jest związane z obniżaniem się energii potencjalnej. Z tego powodu odbierane energii cieplnej z układu jest kompensowane przez energię uzyskiwaną ze zmniejszenia energii potencjalnej. Po całkowitej krystalizacji cieczy temperatura w układzie ulega obniżeniu, co jest związane ze zmniejszaniem się energii kinetycznej cząstek w sieci krystalicznej ciała stałego.
Najczęściej przebieg krzywych chłodzenia nie jest tak prosty tak pokazano to na rysunku powyżej. Najczęściej zakłócenia pojawiają się w tej części krzywej, która odpowiada przejściu gazu w ciecz i cieczy w ciało stałe. Na rysunku obok  pokazano przypadek przemiany cieczy w ciało stałe. Temperatura nie zmienia się wzdłuż linii przerywanej, lecz przebiega wzdłuż linii ciągłej. Ciecz nie krystalizuje w temperaturze krzepnięcia, lecz następuje tzw. przechłodzenie gdzie cząstki cieczy układają się w pewne układy poruszające się w sposób nieuporządkowany. W temperaturze krzepnięcia powinny one utworzyć charakterystyczny dla danej substancji układ krystaliczny. Często zdarza się jednak, że cząstki nie tworzą uporządkowanego układu, lecz w dalszym ciągu poruszają się, a gdy ciepło jest odprowadzane to poniżej temperatury krzepnięcia nadal układ pozostaje w stanie ciekłym. Stan taki jest metastabilny i nawet drobne zaburzenie początkuje proces gwałtownej krystalizacji. Z chwilą gdy w układzie pojawi się odpowiednio duży zarodek krystalizacji wiele cząstek krystalizuje równocześnie, a energia potencjalna ulega przemianie w energię kinetyczną szybciej niż zachodzi odprowadzanie ciepła z układu. W związku z czym cała próbka ulega podgrzaniu do temperatury krzepnięcia.
pokazano przypadek przemiany cieczy w ciało stałe. Temperatura nie zmienia się wzdłuż linii przerywanej, lecz przebiega wzdłuż linii ciągłej. Ciecz nie krystalizuje w temperaturze krzepnięcia, lecz następuje tzw. przechłodzenie gdzie cząstki cieczy układają się w pewne układy poruszające się w sposób nieuporządkowany. W temperaturze krzepnięcia powinny one utworzyć charakterystyczny dla danej substancji układ krystaliczny. Często zdarza się jednak, że cząstki nie tworzą uporządkowanego układu, lecz w dalszym ciągu poruszają się, a gdy ciepło jest odprowadzane to poniżej temperatury krzepnięcia nadal układ pozostaje w stanie ciekłym. Stan taki jest metastabilny i nawet drobne zaburzenie początkuje proces gwałtownej krystalizacji. Z chwilą gdy w układzie pojawi się odpowiednio duży zarodek krystalizacji wiele cząstek krystalizuje równocześnie, a energia potencjalna ulega przemianie w energię kinetyczną szybciej niż zachodzi odprowadzanie ciepła z układu. W związku z czym cała próbka ulega podgrzaniu do temperatury krzepnięcia.
Entropia, potencjał termodynamiczny, przemiana samorzutna
Ogólnie zakłada się, że każdy układ fizyczny dąży do stanu o najniższej energii. Jednak gdy obserwujemy kawałek lodu, który w normalnej temperaturze pokojowej topi się, czyli przechodzi samorzutnie do stanu o energii większej, to zdajemy sobie sprawę, ze jest to wynikiem dostarczania ciepła z otoczenia. Jednak nasuwa się pytanie dlaczego kawałek lodu wykorzystuje pobierane ciepło do topnienia a nie do ogrzewania. Widocznie nie tylko energia cieplna jest potrzebna do określenia kierunku przemiany samorzutnej. Dodatkowym czynnikiem jest skłonność układu do znalezienia się w najbardziej prawdopodobnym stanie, w którym występuje największe nieuporządkowanie cząsteczek. Wynika to z faktu, że istnieje więcej sposobów na nieuporządkowanie układu niż sposobów na jego uporządkowanie. Nieuporządkowanie można ilościowo wyrazić za pomocą entropii. Stan nieuporządkowany ma większą entropię niż stan uporządkowany. Oczywistym jest, że woda w stanie ciekłym jest bardziej nieuporządkowana niż woda w postaci lodu. Stany o większej entropii są bardziej prawdopodobne niż stany o entropii mniejszej. W lodzie występuje jeden jedyny sposób ułożenia cząsteczek wody, w wodzie ciekłej takich stanów są miliony, a każdy z nich tak samo prawdopodobny. Z tego wynika, że najbardziej naturalne są procesy w których następuje spadek energii jak również i te w których następuje wzrost entropii. W przypadku topnienia lodu występują obydwa te przeciwstawne procesy. Powyżej temperatury topnienia przeważa wzrost entropii, poniżej tej temperatury przeważa spadek energii i dlatego woda krzepnie. Temperatura jest więc czynnikiem krytycznym, który decyduje o tym jak ważny jest wzrost entropii w stosunku do spadku energii. W temperaturze 0K entropia jest równa 0, czyli najtrwalszym stanem jest stan o najniższej energii. Gdy temperatura wzrasta nasila się ruch cząsteczek i tendencja nieuporządkowania staje się coraz istotniejsza dla zachodzenia procesów. Wzajemne oddziaływanie entropii i energii można ująć ilościowo stosując pojęcie potencjału termodynamicznego (energii swobodnej). W takim ujęciu energia całkowita jest równa potencjałowi termodynamicznemu (G) + TS (S - entropia). Należy pamiętać, że w energii całkowitej mieści się również energia zewnętrzna równa iloczynowi PV, gdyż substancje zajmują pewną objętość V i są pod pewnym ciśnieniem P. Suma energii wewnętrznej i pracy zewnętrznej jest równa entalpii (H). Stąd potencjał termodynamiczny wyraża się zależnością:
G = H – TS
Istotne znaczenie mają nie absolutne wartości potencjału G ale ich zmiany. Czyli przyrost G ma postać:
ΔG = ΔH – TΔS.
Zgodnie z tym w danej temperaturze i pod stałym ciśnieniem reakcja chemiczna lub przemiana fizyczna może następować samorzutnie tylko w przypadku gdy towarzyszy jej spadek potencjału termodynamicznego. Innymi słowy wartość ΔG powinna być ujemna czyli w stanie końcowym wartość potencjału G musi być mniejsza niż w stanie początkowym procesu samorzutnego. Ujemną wartość ΔG wywołuje albo zmniejszenie entalpii lub wzrost entropii. Wartość ΔH < 0 odpowiada procesowi korzystnemu pod względem energetycznym, czyli takiemu w którym energia maleje. Natomiast ΔS > 0 odpowiada procesowi, w którym rośnie nieporządek w układzie. Dla wielu procesów, takich jak topnienie ciał stałych ΔH i ΔS mają ten sam znak czyli w takich wypadkach to temperatura odgrywa decydującą rolę przy samorzutnym zachodzeniu takich procesów.
