Wiązania metaliczne

Pierwsza, klasyczna teoria wiązań występujących w metalach powstała w roku 1900, a jej twórcami byli Paul Karl Ludwig Drude i Hendrik Lorentz. Zgodnie z tą teorią elektrony walencyjne metalu mają zdolność do swobodnego poruszania się we wszystkich kierunkach. W związku z tym we wnętrzu metalu, w każdym punkcie, panuje jednakowy potencjał. Skokowa zmiana potencjału następuje dopiero na powierzchni metalu. W takich warunkach energia elektronów we wnętrzu metalu zależy jedynie od ich energii kinetycznej, a rozkład energii opisuje statystyka Maxwella-Boltzmanna. Podany przez twórców model dobrze opisuje właściwości metali takie jak przewodnictwo elektryczne będące wynikiem swobodnego ruchu elektronów. Dodatkowo teoria Drudego wiąże przewodnictwo cieplne metali z liczbą elektronów swobodnych, ich średnią prędkością i drogą swobodną. Jednak prowadzi ona do wniosków niezgodnych z wartościami ciepła atomowego metali. Gaz elektronowy w metalu zgodnie z tą teorią powinien wykazywać właściwości gazu doskonałego, a w związku z tym pojemność cieplna metalu powinna zależeć nie tylko od oscylacyjnych stopni swobody atomów tworzących metal lecz również od translacyjnych stopni swobody gazu elektronowego. Niestety wyznaczone na tej podstawie wartości ciepła atomowego metali nie zgadzają się z wartościami wyznaczonymi eksperymentalnie.

Teoria Drudego została zmodyfikowana przez A. Sommerfelda na gruncie mechaniki kwantowej. W poprawionej teorii zachowane zostało założenie, że energia potencjalna elektronów we wnętrzu metalu ma stałą wartość (przyjmuje się, że jest równa 0), ale zachowanie elektronów opisuje funkcja falowa. W takim wypadku problem opisu elektronu we wnętrzu metalu sprowadza się do problemu cząstki w pudle potencjału, a energia elektronu może przyjmować tylko określone wartości. Liczba stanów energetycznych, a tym samym i kwantowych charakteryzuje się różnymi zespołami liczb zawartymi w przedziale od E do E + dE, a uwzględnienie spinu jeszcze podwaja ten zbiór stanów. Oczywiście rozmieszczenie elektronów na dopuszczalnych poziomach energetycznych podlega zakazowi Pauliego, co powoduje, że ich rozkład jest opisywany statystyką Fermiego-Diraca. W temperaturze bliskiej zeru bezwzględnemu elektrony zajmują przede wszystkim najniższe poziomy energetyczne, co powoduje, że zapełnione całkowicie sa stany o energiach od zera do pewnej wartości granicznej zwanej poziomem Fermiego. Powyżej poziomu Fermiego znajdują się stany nie obsadzone elektronami. Liczbę stanów kwantowych pomiędzy zerem a energią stanu Fermiego (E_F) jest równa liczbie swobodnych elektronów N w objętości V:

a stąd energia poziomu Fermiego wynosi:

Średnia energia elektronu swobodnego wynosi 3/5E_F. Jak widać zastosowanie mechaniki kwantowej do opisu elektronów w metalu pokazuje, że ich energia w temperaturze zera bezwzględnego jest większa od zera. natomiast w klasycznym modelu opartym o statystykę Maxwella-Boltzmanna energia ta była równa 0. W miarę wzrostu temperatury oczekujemy, że elektrony będą przechodzić na wyższe niż E_F poziomy energetyczne. Jednak proces taki napotyka pewna trudność. Otóż energia przekazywana elektronom wraz ze wzrostem temperatury wynosi kT, co pozwala na przechodzenie na wyższe poziomy elektronom, których energia jest większa niż E_F – kT. Pozostałe elektrony o energiach znacznie poniżej poziomu Fermiego mają bardzo małe prawdopodobieństwo do przejścia na wyższe poziomy energetyczne jak długo E_F » kT. W związku z tym gaz elektronowy znajduje się w stanie zwyrodniałym czyli zdegenerowanym. To wyjaśnia dlaczego udział pojemności cieplnej gazu elektronowego jest niewielki, około 1%,  w całkowitej pojemności cieplnej metalu.

Teoria pasmowa ciała stałego

Model oparty na teorii swobodnych elektronów wyjaśnia w dobry sposób szereg właściwości metali, ale nie daje wyjaśnienia różnicy pomiędzy metalami, półprzewodnikami i przewodnikami. Ta słabość teorii wynika z przyjęcia w założeniu braku oddziaływania pomiędzy elektronami a siecią przestrzenną kryształu. Dopuszczenie takie oddziaływania prowadzi do teorii pasmowej ciała stałego. Sieć przestrzenna musi być ro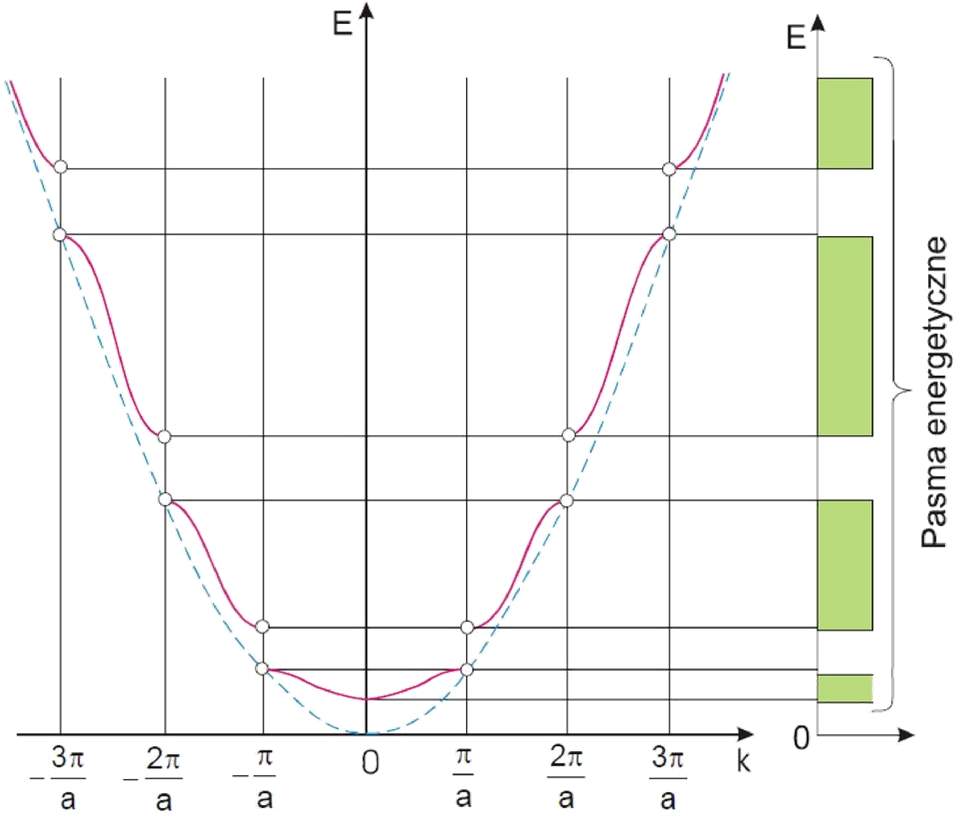Zależność energii kinetycznej elektronów od wektora falowego w całej przestrzeni kryształu.zpatrywana jako układ elektronów poruszających się w polu dodatnio naładowanych jąder znajdujących się w węzłach sieci. Do opisu takiego układu można zastosować równanie Schrödingera, w którym funkcja falowa, na którą działa operator jest funkcją współrzędnych wszystkich elektronów zawartych w krysztale. Po przyjęciu odpowiednich przybliżeń dotyczących oddziaływań pomiędzy elektronami, czyli zastąpienia rzeczywistych oddziaływań elektron–elektron wypadkowym polem sił, w którym każdy elektron porusza się niezależnie od pozostałych. Dodatkowo zastosowanie uproszczenia Sommerfelda, czyli przyjęcie stałego potencjału wewnątrz kryształu, prowadzi do pierwszego modelu Blocha, w którym elektrony poruszają się niezależnie od siebie w polu zrębów atomowych złożonych z jąder otoczonych zamkniętymi powłokami elektronowymi. Model ten postuluje występowanie w krysztale pasm energetycznych, zajmowanych przez elektrony oraz pasm wzbronionych.

Do podobnych wniosków prowadzi także podejście oparte o falową naturę elektronu. Energia elektronu poruszającego się swobodnie z prędkością v wynosi: E =½ m·v² = p²/2m. Pęd p możemy związać z długością fali de Broglie’a: p=m·v=h/λ=(2π/λ) ℏ. Ponieważ elektron traktujemy jak falę, to w krysztale obowiązuje równanie Braggów: nλ =2dsinθ. Innymi słowy elektron swobodny poruszający się wewnątrz kryształu ulega odbiciu od pewnych płaszczyzn, w sytuacji gdy jego wektor falowy (2π/λ) będzie tak dobrany aby spełnione zostało równanie Braggów. Z tego wynika, że nie wszystkie wartości energii elektronu są dopuszczalne, a obszary gdzie funkcja energii w trójwymiarowym krysztale jest nieciągła prezentują strefy Brillouina. Otrzymujemy w ten sposób taki sam model jak przy rozpatrywaniu funkcji falowej.  

Istotną rolę w przypadku półprzewodników odgrywają zanieczyszczenia lub defekty kryształów, które powodują wystąpienie dodatkowych poziomów energetycznych i wpływają na wielkość przerwy energetycznej pomiędzy pasmem podstawowym i przewodzenia.