Teoria pola ligandów

Teoria pola ligandów jest zasadniczo teorią orbitali cząsteczkowych zastosowaną do związków koordynacyjnych, na gruncie której jest możliwe wyjaśnienie wiązania kowalencyjnego w związkach koordynacyjnych, jak również analiza widm elektronowych związków koordynacyjnych. Ponadto teoria umożliwia wyjaśnienie stabilności związków koordynacyjnych, w szczególności daje podstawy teoretyczne do reguły 18-elektronów łącznie z wyjaśnieniem występowania odstępstw od tej empirycznej reguły. Podobnie jak w teorii orbitali cząsteczkowych, stosujemy tutaj liniową kombinację orbitali atomowych opartą na symetrii przy konstruowania orbitali cząsteczkowych związków koordynacyjnych. Jednak podejście to jest nieco zmodyfikowane. W pierwszym kroku określamy grupę punktową cząsteczki i przypisujemy osie układu współrzędnych w sposób najbardziej użyteczny. W drugim kroku określamy orbitale walencyjne, zwane także orbitalami granicznymi metalu. Na przykład, dla metalu przejściowego z czwartego okresu rozważymy orbitale 4s, 4p i 3d jako graniczne. Następnie określamy symetrię tych orbitali. Możemy to zrobić posługując się tabelami charakterów odpowiedniej grupy punktowej. W kolejnym kroku wybieramy orbitale ligandów o najwyższej energii, które są odpowiednie do utworzenia wiązania σ. W przypadku ligandów, które są cząsteczkami lub jonami wieloatomowymi, są to orbitale HOMO o symetrii odpowiedniej do utworzenia wiązania σ. W przypadku prostych jonów, takich jak ligandy halogenowe, są to najwyższe zajęte orbitale atomowe. Następnie grupujemy wybrane orbitale ligandów w celu utworzenia odpowiednich orbitali (LGO) i określamy ich typy symetrii. Aby to zrobić, określamy reprezentację i doprowadzamy ją do reprezentacji nieredukowalnej. To daje nam typy symetrii orbitali grup ligandów. Następnie łączymy orbitale graniczne metalu i orbitale ligandów o tym samym typie symetrii, aby utworzyć orbitale cząsteczkowe. Mając skonstruowane wszystkie orbitale cząsteczkowe odpowiednie do utworzenia wiązania σ możemy narysować diagram orbitali cząsteczkowych obejmujący wiązania σ w związku koordynacyjnym. Następnie szukamy orbitali ligandów, które są odpowiednie do utworzenia wiązania π z metalem. Określamy typy symetrii grup orbitali ligandów. Orbitale ligandów i orbitale metalu o tej samej symetrii łączymy, aby utworzyć orbitale cząsteczkowe, które reprezentują wiązanie π w cząsteczce. Orbitale te wprowadzamy do diagramu orbitali cząsteczkowych związku. Na koniec sprawdzamy, czy istnieją orbitale ligandów odpowiednie do utworzenia wiązania δ z metalem. Jeśli tak, tworzymy dla nich również grupę orbitali ligandów, określamy ich typy symetrii i łączymy orbitale ligandów i orbitale metalu o tej samej symetrii, aby utworzyć orbitale cząsteczkowe. W ostatnim kroku dodajemy je do diagramu orbitali cząsteczkowych.

Zastosujmy teorię pola ligandów do oktaedrycznego kompleksu metalu przejściowego czwartego okresu. Zgodnie z regułami musimy najpierw określić grupę punktową i zdefiniować układ współrzędnych; grupa punktowa to oczywiście O_h.

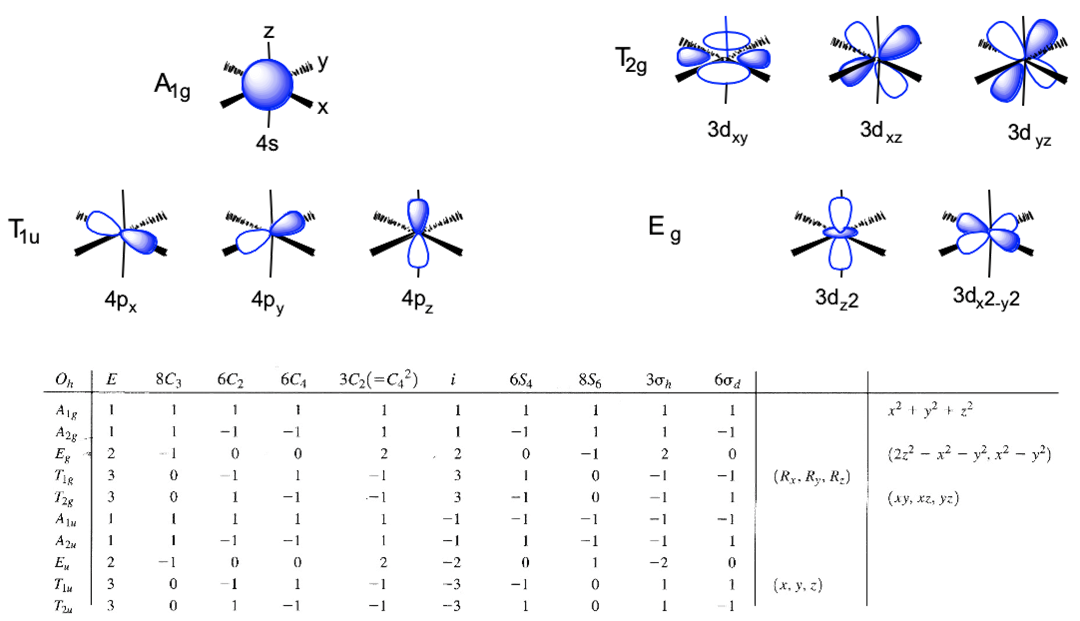Kontury orbitali atomu metalu oraz tabela charakterów grupy punktowej Oh.

Układ współrzędnych zdefiniujemy tak, aby ligandy leżały na osiach x, y i z. Graniczne (walencyjne) orbitale metalu to 4s, 4p i 3d, musimy zatem określić ich symetrię. W tym celu wykorzystamy tabelę charakterów grupy O_h. Orbital s jest oczywiście sferycznie symetryczny, w tabeli charakterów ten typ symetrii zawsze znajduje się na pierwszej pozycji, a w grupie O_h odpowiada mu symetria A_1g. Zobaczmy jakiego rodzaju symetria opisuje orbitale 4p. Symbole x, y i z znajdują się w nawiasie przy nieprzywiedlnej reprezentacji typu symetrii T_1u. Oznacza to, że trzy orbitale 4p są potrójnie zdegenerowane i mają symetrię typu T_1u. Na koniec musimy określić typy symetrii orbitali 3d. Znajdujemy xy, xz i yz przy nieprzywiedlnej reprezentacji T_2g. Zatem te orbitale mają symetrię typu T_2g. Dalej znajdujemy 2z²-x²-y² i x²-y² przy reprezentacji E_g, zatem orbitale d_z2 i d_x2-y są zdegenerowane i mają typ symetrii E_g. Wyrażenie 2z²-x²-y² matematycznie opisuje stożek, a orbital d_z2 ma węzeł w wierzchołku stożka, zatem znaleźliśmy wszystkie typy symetrii orbitali granicznych atomu centralnego.

Następnie musimy rozpatrzeć ligand i znaleźć najwyższy zajęty orbital cząsteczkowy lub atomowy zdolny do utworzenia wiązania σ. Oczywiście zależy to od rodzaju liganda. Jako przykład weźmy pod uwagę tlenek węgla(II), czyli ligand karbonylowy CO. Aby określić jego poziom HOMO odpowiedni do utworzenia wiązania σ z metalem, najpierw będziemy musieli skonstruować diagram orbitali cząsteczkowych tlenku węgla(II). Cząsteczka CO jest liniową, polarną cząsteczką należącą do grupy punktowej C_∞v.

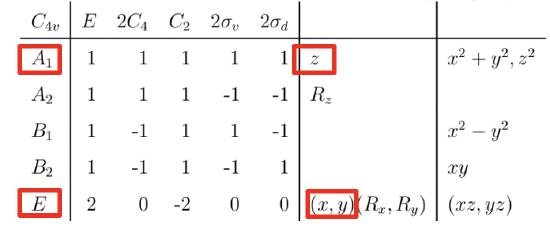Tabela charakterów grupy punktowej C4v.

Tablica charakterów grupy punktowej C_∞v jest kłopotliwa w użyciu ze względu na nieskończoną krotność osi głównej i nieskończoną liczbę płaszczyzn symetrii. Dlatego zamiast tego użyjemy podgrupy C_4v. Podgrupa grupy to grupa, która powstaje, gdy usuniemy pewne elementy symetrii z grupy nadrzędnej. Przy tym działaniu należy zachować ostrożność aby nie przeoczyć degeneracji orbitali cząsteczkowych, co może zajść, gdy zbytnio zmniejszymy symetrię. Grupa punktowa C_4v to grupa punktowa o najniższej symetrii, jaką możemy wybrać bez przeoczenia degeneracji. Zasadniczo jest to spowodowane tym, że orbitale atomowe C i O mają na powłoce walencyjnej tylko orbitale 2s i 2p, a orbitale 2p prostopadłe do osi wiązania C–O przy obrocie o 90° przekształcają się wzajemnie w siebie. Takie przekształcenie wymaga osi obrotu rzędu czwartego. Gdybyśmy wybrali grupę punktową C_2v, która ma niższą symetrię, nadal bylibyśmy w stanie skonstruować diagram orbitali cząsteczkowych, ale nie bylibyśmy w stanie wykazać degeneracji orbitali 2p_x i 2p_y. W celu określenia typów symetrii orbitali walencyjnych C i O posiłkujemy się tabelą charakterów grupy C_4v. Łatwo stwierdzić, że orbitale 2s i 2p_z mają symetrię typu A₁, a orbitale 2p_x i 2p_y są zdegenerowane i mają symetrię typu E. Teraz możemy połączyć orbitale atomowe, tworząc orbitale cząsteczkowe.

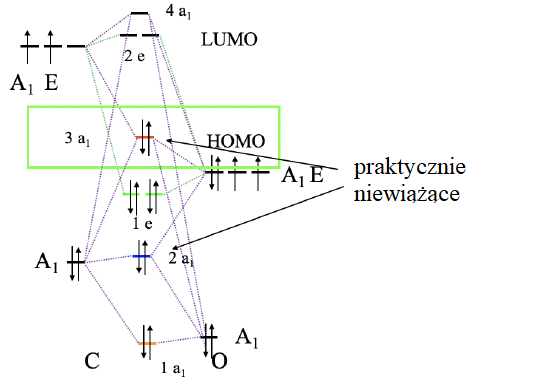Diagram orbitali cząsteczkowych CO

Aby skonstruować diagram orbitali cząsteczkowych, musimy wziąć pod uwagę, że O jest znacznie bardziej elektroujemny niż C, a zatem orbital 2s O ma mniejszą energię niż 2s węgla. Orbitale 2p O mają niższą energię niż 2p węgla. Po określeniu symetrii łączymy orbitale o tym samym typie symetrii tworząc diagram orbitali cząsteczkowych. Skonstruowany diagram wypełniamy elektronami. Cztery elektrony pochodzą od węgla a sześć od tlenu, co daje w sumie dziesięć elektronów. Oznacza to, że orbitale cząsteczkowe 1a₁, 2a₁, 1e₁ i 3a₁ są zapełnione. Zatem HOMO jest umiejscowiony na poziomie 3a₁, który  ze względu na symetrię może tworzyć wiązanie σ z metalem.

W następnym kroku musimy zgrupować sześć orbitali HOMO tlenku węgla, aby utworzyć orbitale grupy ligandów i określić ich typy symetrii. Odbywa się to poprzez najpierw określenie przywiedlnej reprezentacji orbitali, a następnie określenie liczby nieprzywiedlnych reprezentacji danego typu za pomocą procedury redukcyjnej teorii grup. Nie wnikając w szczegóły uzyskujemy jeden orbital o symetrii a_1g, dwa dwukrotnie zdegenerowane orbitale ligandów o symetrii e_g, i trzy trójkrotnie zdegenerowane orbitale ligandów o symetrii t_1u. Orbital a_1g jest całkowicie symetryczny. Orbitale t_1u mają jeden węzeł, a e_g dwa węzły. Znając typy symetrii orbitali granicznych atomu centralnego (metal) i orbitale grupy ligandów możemy skonstruować jakościowy diagram cząsteczki ML6 o oktaedrycznej geometrii wielościanu koordynacyjnego.

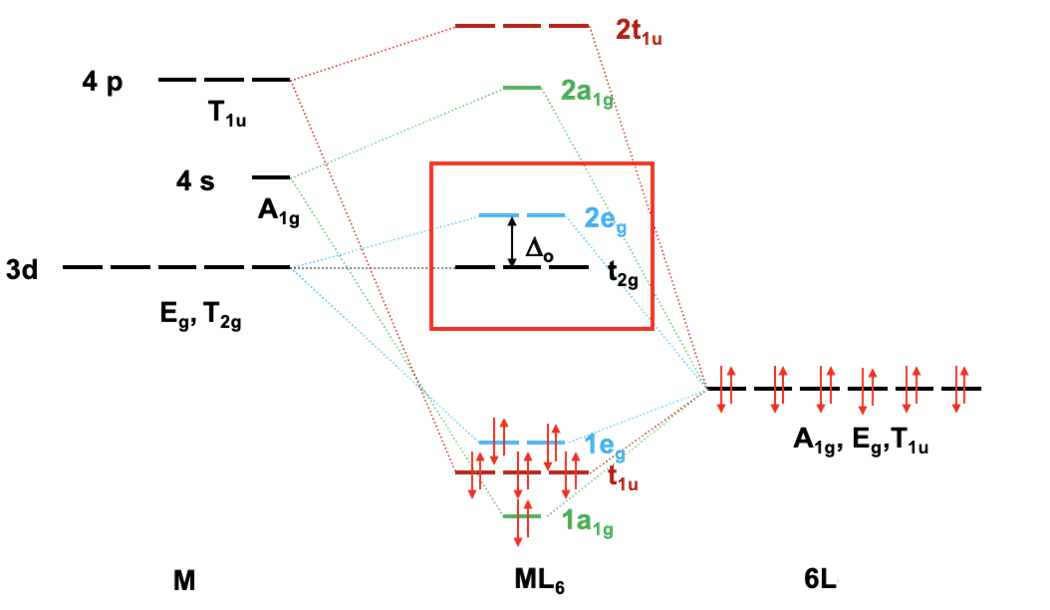Diagram orbitali cząsteczkowych dla kompleksu oktaedrycznego metalu przejściowego z IV okresu (tylko wiązanie σ).

Dla metalu przejściowego czwartego okresu kolejność energii poziomów jest następująca 3d < 4s < 4p. Rozsądne jest założenie, że orbitale grupy ligandów mają mniej więcej taką samą energię jak orbitale 3d metalu. Następnie możemy przypisać orbitalom ich wcześniej określone typy symetrii i połączyć orbitale o tych samych typach symetrii w celu utworzenia orbitali cząsteczkowych. Możemy zacząć od orbitali o symetrii typu A₁. Orbital 4s ma ten typ symetrii. Również jeden orbital grupy ligandów jest tego typu. Dlatego spodziewalibyśmy się jednego wiążącego i jednego antywiążącego orbitalu cząsteczkowego; oznaczymy je odpowiednio 1a_1g i 2a_1g. Następnie rozważmy orbitale o symetrii E_g. Istnieją dwa orbitale d metalu i dwa orbitale grupy ligandów o tej symetrii. Dlatego tworzymy dwa dwukrotnie zdegenerowane wiążące i dwa dwukrotnie zdegenerowane antywiążące poziomy, odpowiednio 1e_g i 2e_g. Istnieją trzy orbitale 4p metalu o symetrii T_1u, które możemy połączyć z orbitalami ligandów o tej samej symetrii. Otrzymujemy trójkrotnie zdegenerowane orbitale wiążące i antywiążące o symetrii t_1u. Wreszcie pozostają orbitale metalu T_2g, ale brak jest orbitali ligandów o tej samej symetrii, dlatego orbitale T_2g pozostają niewiążące.

Mamy już diagram orbitali cząsteczkowych, ale nadal musimy wypełnić go elektronami. Traktujemy wiązanie metal-ligand jako donorowo-akceptorowe, przy czym pary elektronów są pochodzą z HOMO liganda. Oznacza to, że mamy do rozważenia ogółem 6x2 = 12 elektronów. Teraz wszystko zależy od tego, jaki mamy jon metalu. Załóżmy, że mamy jon metalu d⁰. Oznacza to, że w sumie mamy 12 elektronów, które lokalizujemy na orbitalach 1a_1g, t_1u i 1e_g. Teraz załóżmy, że mamy jonu metalu o konfiguracji d¹⁰. Wtedy zajmowane są orbitale t_2g i 2e_g. Orbitale t_2g to niewiążące orbitale d_xz, d_xy i d_yz metalu. Orbitale 2e_g to orbitale cząsteczkowe, w których dominują orbitale d_z2 i d_x2-y2. Możemy zatem powiedzieć, że orbitale t_2g i 2e_g są orbitalami d poddanymi wpływowi oktaedrycznego pola ligandów. Ze względu na obecność pola ligandów energie orbitali d netalu rozszczepiają się, a różnica w ich energii jest energią rozszczepienia oktaedrycznego pola ligandów Δ. Widać tutaj analogię do teorii pola krystalicznego.

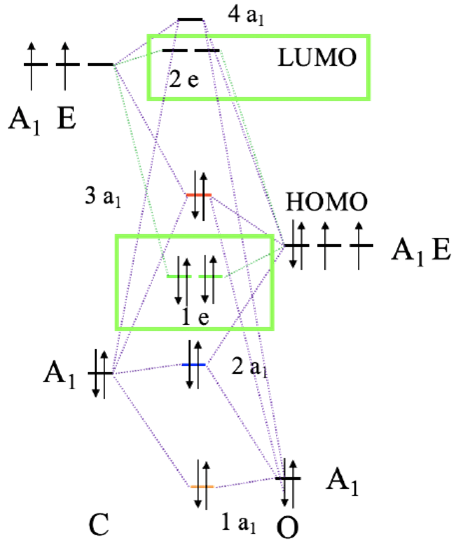Diagram orbitali cząsteczkowych CO z zaznaczeniem (kolor zielony) orbitali mogących tworzyć wiązania π z metalem

Rozważmy wiązanie π w kompleksie oktaedrycznym. Musimy w tym celu znaleźć orbitale liganda mające odpowiednią symetrię, i energię, do utworzenia wiązania π z metalem. Dalej rozważamy ligand karbonylowy, dlatego musimy ponownie przyjrzeć się diagramowi orbitali cząsteczkowych CO i sprawdzić, czy istnieją orbitale molekularne odpowiednie do utworzenia wiązania π. W cząsteczce CO orbitale 1e i 2e są orbitalami wiążącymi i antywiążącymi π, co wynika z ich konstrukcji opartej na orbitalach 2p_x i 2p_y. Każdy ligand ma dwa orbitale 1e i dwa 2e, co daje w sumie cztery orbitale. Te orbitale są energetycznie zbliżone do HOMO, zatem można przypuszczać, że ich energie odpowiadają energii orbitali d jonu centralnego. Orbitale 1e to wiążące orbitale π, a 2e to orbitale antywiążące π*.

Wiązanie π w oktaedrycznym kompleksie karbonylowym metalu przejściowego z 4 okresu

Grupujemy dwanaście orbitali wiążących (6 ligandów po jednym, dwukrotnie zdegenerowanym poziomie 1e), aby utworzyć jeden zestaw orbitali ligandów, i grupujemy dwanaście orbitali antywiążących, aby utworzyć drugi zestaw orbitali ligandów. Określamy typy symetrii każdego zbioru znajdując, że dwanaście orbitali wiążących ligandów ma symetrię T_1g, T_2g, T_1u i T_2u. Dwanaście orbitali antywiążących ligandów ma te same typy symetrii. Teraz, gdy określiliśmy typy symetrii orbitali grup ligandów dostępnych do wiązania π, musimy wybrać te orbitale grup ligandów, które mają odpowiednią symetrię, aby utworzyć orbitale cząsteczkowe z orbitalami d metalu w oktaedrycznym polu ligandów. Są to poziomy  2e_g i t_2g. Orbitale ligandów mają odpowiednio symetrię T_1g, T_2g, T_1u i T_2u. Oznacza to, że możemy połączyć orbitale metalu t_2g i orbitale ligandów o symetrii T_2g, aby utworzyć orbitale cząsteczkowe. Orbitale e_g metalu i orbitale ligandów o symetrii T_1g, T_1u i T_2u pozostają niewiążące. Trzy wiążące orbitale T_2g ligandów utworzą sześć orbitali cząsteczkowych z trzema orbitalami t_2g metalu. Musimy wziąć pod uwagę, że istnieją również trzy antywiążące orbitale ligandów o symetrii T_2g^*, powstające z antywiążących orbitali π. One również mogą oddziaływać z orbitalami t_2g metalu. Orbitale o symetrii T_1u^*, T_1g^* i T_2u^* są niewiążące.

Przeanalizujmy dwa skrajne przypadki oddziaływania poziomu t_2g metalu z orbitalami ligandów o symetrii T_2g i T_2g^*. W pierwszym przypadku orbitale T_2g ligandów mają energię zbliżoną do energii orbitali t_2g metalu, a T_2g^*  ligandów mają energię znacznie wyższą niż poziom t_2g metalu. W tym przypadku możemy pominąć oddziaływanie kowalencyjne między orbitalami T_2g^* ligandów i poziomem t_2g metalu, a orbitale T_2g^* pozostają niewiążące. Bierzemy pod uwagę tylko oddziaływanie między T_2g ligandów i t_2g metalu w celu utworzenia trzech wiążących i trzech antywiążących orbitali cząsteczkowych o symetrii t_2g. Teraz rozważmy elektrony. Orbitale T_2g ligandów są  zapełnione, dlatego należy wziąć pod uwagę łącznie sześć elektronów. Te sześć elektronów trafiłoby do trzech wiążących orbitali cząsteczkowych t_2g. Dalej możemy mieć do dziesięciu elektronów d metalu. Sześć z nich trafi na orbitale t_2g zlokalizowane na metalu, a pozostałe cztery na orbitale e_g. Po utworzeniu wiązania π, elektrony atomu centralnego t_2g pozostaną niewiążące. Zatem wiązania π obniżają energię elektronów ligandów, ale zwiększają energię elektronów metalu. Stabilizacja netto energii elektronów, będzie zależeć od tego, ile mamy elektronów d. Tak długo, jak będzie mniej niż sześć elektronów d, będziemy obserwować stabilizację, jeśli będzie ich więcej, nastąpi ogólna destabilizacja. Możemy również zapytać, jaki wpływ ma wiązanie π na wielkość rozszczepienia Δ, i łatwo się zorientować, że wiązanie π zmniejsza wielkość parametru Δ.

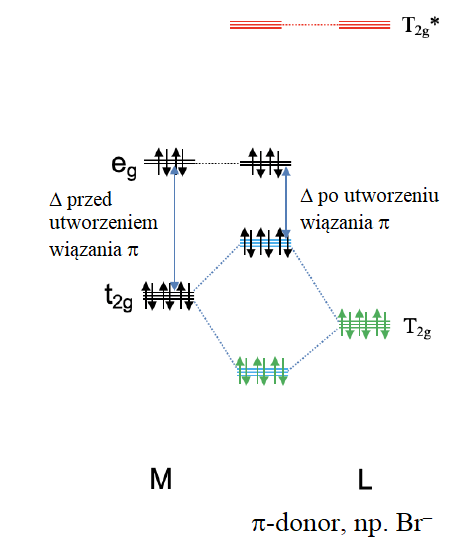Wpływ liganda π-donorowego na Δ na przykładzie jonu d10.

Rozważmy teraz odwrotny przypadek, w którym orbitale antywiążące T_2g^* ligandów mają energię zbliżoną do energii poziomu t_2g metalu, a orbitale wiążące T_2g ligandów są na tyle nisko energetyczne aby znacząco oddziaływać z orbitalami t_2g. Oznacza to, że orbitale T_2g pozostają praktycznie niewiążące. Orbitale ligandów T_2g^* i orbitale t_2g metalu tworzą potrójnie zdegenerowane orbitale cząsteczkowe wiążące i odpowiadające im orbitale cząsteczkowe antywiążące. Orbitale ligandów T_2g^* są pozbawione elektronów, więc na wiążące orbitale cząsteczkowe o symetrii t_2g można wprowadzić do sześciu elektronów d metalu. Wszelkie pozostałe  elektrony podpowłoki d metalu zostają zlokalizowane na poziomie e_g. Widzimy, że w przeciwieństwie do poprzedniego przypadku, możemy obniżyć energię elektronów d metalu w wyniku utworzenia wiązania π. Ponieważ elektrony wiążące t_2g są współdzielone między metalem a ligandem, gęstość elektronowa zostaje przeniesiona od metalu do ligandów. Dlatego ligand, który głównie wykorzystuje swoje antywiążace orbitale T_2g^* do tworzenia wiązania π, nazywany jest ligandem π-akceptorowym, przyjmuje on gęstość elektronową d od metalu. Przykładem liganda π-akceptorowego jest ligand karbonylowy.

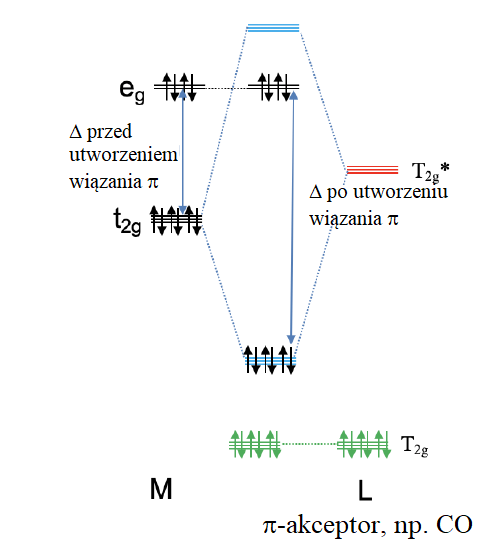Wpływ liganda π-akceptorowego, np. CO, na Δ

Omówiliśmy dwa skrajne przypadki, jednak istnieje spektrum ligandów o właściwościach silnie π-donorowych do silnie π -akceptorowych. Możliwe jest również, że efekty π-donorowe i π-akceptorowe znoszą się wzajemnie. Dzieje się tak, gdy orbitale T_2g i T_2g^* ligandów znajdują się na skali energii w przybliżeniu w równej odległości od orbitali t_2g metalu. Niektóre ligandy w ogóle nie mają orbitali zdolnych do tworzenia wiązania π.

Wpływ wiązania π na parametr rozszczepienia Δ obrazuje szereg spektrochemiczny ligandów. Ponieważ ligandy π-akceptorowe zwiększają Δ, kompleksy metali z takimi ligandami absorbują światło o krótszej długości fali i wyższej energii. Ligandy π-donorowe zmniejszają wartość Δ, a tym samym kompleksy z nimi pochłaniają światło o niższej energii. Zmiany wielkości parametru rozszczepienia w polu ligandów są skorelowane z właściwościami magnetycznymi związków koordynacyjnych. Zgodnie z teorią pola ligandów π-akceptory tworzą kompleksy o niskim spinie, a π-donory tworzą kompleksy o wysokim spinie.

Inną cechą teorii pola ligandów jest to, że może ona wyjaśnić regułę 18 elektronów oraz wyjątki od tej reguły. Na przykład oktaedryczny kompleks heksakarbonylochromu jest kompleksem 18-elektronowym. Skonstruujmy jakościowy molekularny diagram orbitalny i zobaczmy, czy diagram MO potwierdza stabilność kompleksu. Diagram MO uwzględniający tylko oddziaływania σ przedstawiono wyżej. Widzimy, że wszystkie dwanaście elektronów ligandów znajduje się w wiążących orbitalach cząsteczkowych 1_a1, 1t_u i 1e_g. Ponadto chrom ma sześć elektronów walencyjnych. Te elektrony pozostają niewiążące, gdy rozważa się tylko wiązania σ. Jednak sytuacja ulega zmianie, gdy weźmiemy pod uwagę wiązania π. Ligand CO jest silnym ligandem π-akceptorowym, dlatego w wiązaniu rozważamy tylko orbitale ligandów T_2g^* o symetrii π. Znajdują się one energetycznie powyżej orbitali ligandów tworzących wiązania σ. Orbitale d metalu, o symetrii T_2g, tworzą trzy wiążące cząsteczkowe orbitale t_2g i trzy antywiążące. Ponieważ możemy wprowadzić elektrony d metalu na wiążące orbitale cząsteczkowe, stan elektronów d zmienia się z niewiążącego na wiążący. Widzimy teraz, że wszystkie 18 elektronów znajduje się na wiążących orbitalach cząsteczkowych. Kiedy wszystkie elektrony w cząsteczce znajdują się na orbitalach cząsteczkowych wiążących cząsteczka związku jest stabilna. To wyjaśnia, dlaczego kompleksy 18-elektronowe są stabilne.

Jakościowy diagram MO oktaedrycznego kompleksu heksakarbonylchrom(0) z uwzględnieniem wiązania π.

Teraz skonstruujmy diagram orbitali cząsteczkowych dla WCl₆. To nie jest kompleks 18-elektronowy, ma tylko dwanaście elektronów pochodzących z sześciu ligandów chlorowych. Wolfram jest na +6 stopniu utlenienia, i nie posiada elektronów na podpowłoce d ⁰. Zobaczmy jak teoria pola ligandów może wyjaśnić ten wyjątek od reguły 18 elektronów. Zacznijmy ponownie od diagramu MO z uwzględnieniem tylko wiązania σ. Dwanaście elektronów ligandów umieszczamy na orbitalach wiążących 1a_1g, 1t_u i 1e_g. Niewiążące orbitale t_2g i antywiążące orbitale 2e_g pozostają puste z powodu braku elektronów d metalu. Widzimy, że wszystkie wiążące orbitale cząsteczkowe są zapełnione, a wszystkie pozostałe puste, co wyjaśnia stabilność cząsteczki, a tym samym wyjątek od reguły 18 elektronów. Rozważmy teraz dodatkowo wiązanie π. Ligand chlorowy jest typowym donorem π, który wykorzystuje elektrony 3p, z orbitali o symetrii odpowiedniej do utworzenia wiązania π. Z tego powodu rozważamy tylko orbitale T_1g grupy ligandów. Te orbitale są zapełnione elektronami, ponieważ anion chlorkowy ma pełną podpowłokę 3p. Interakcja LGO T_2g z orbitalami t_2g metalu tworzy wiążący t_2g i antywiążący t_2g^* orbital cząsteczkowy. Elektrony π ligandów mają teraz mniejszą energię niż w przypadku gdy wiązanie π z metalem nie istnieje. Z tego powodu wiązanie π dodatkowo ustabilizowało kompleks. W pewnym sensie możemy teraz stwierdzić, że mamy kompleks 18-elektronowy, ponieważ kiedy dodamy 6 elektronów π do 12 elektronów σ, otrzymamy w sumie 18 elektronów wiążących. Te dodatkowe 6 elektronów nie są uwzględniane w zliczaniu elektronów, ponieważ procedura zliczania elektronów traktuje wiązanie W–Cl jako pojedyncze i bierze pod uwagę tylko odziaływanie σ między W i Cl.

Jakościowy diagram orbitali cząsteczkowych WCl6 z uwzględnieniem wiązania π.

Związki o tetraedrycznym i kwadratowym wielościanie koordynacyjnym omówione zostały na kolejnej stronie