Teoria pola ligandów

Opracowanie teorii pola krystalicznego i pola ligandów jest dostępne w postaci dokumentu pdf w tym miejscu.

Związki o geometrii tetraedrycznej

Rozważmy związek o tetraedrycznej geometrii wielościanu koordynacyjnego. Grupa punktowa dla tetraedru to T_d i potrzebujemy tabeli charakterów tej grupy punktowej.

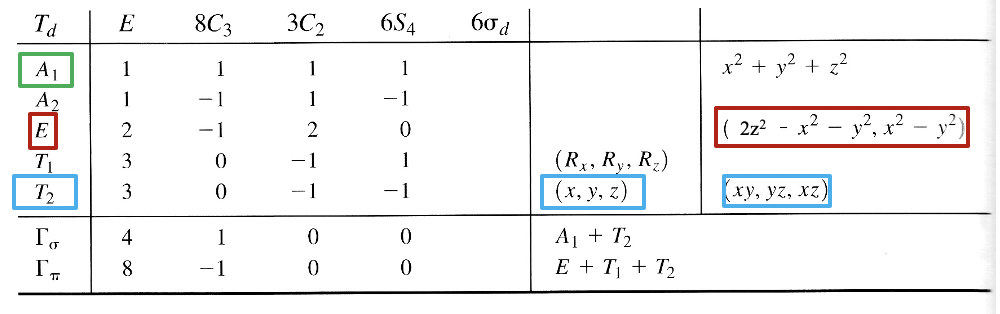Tabela charakterów grupy Td

Wybieramy układ współrzędnych wpisując czworościan w sześcian, wstawiając w co drugi wierzchołek sześcianu ligand. Osie współrzędnych przebiegają prostopadle do ścian sześcianu.

Teraz musimy określić typy symetrii orbitali granicznych metalu. W przypadku czwartego okresu orbitalami walencyjnymi są 3d, 4s i 4p. Orbital 4s jest pełnosymetryny typu A₁, Znajdujemy litery x, y i z w nawiasach w niprzywiedlnej reprezentacji typu T₂, a to oznacza, że ​​orbitale 4p są potrójnie zdegenerowane i mają typ symetrii T₂. Orbitale 3d_xy, 3d_yz i 3d_xz znajdują się w tej samej reprezentacji, są również potrójnie zdegenerowane i też mają symetrię T₂. Orbitale 3d_x2-y2 i 3d_z2 mają symetrię typu E zgodnie z tabelą charakterów dla tej grupy punktowej.   Zajmiemy się ligandami. Ponieważ najpierw musimy rozważyć wiązanie σ, należy znaleźć HOMO liganda odpowiednie do utworzenia wiązania σ. Wybierzemy ligand karbonylowy jako przykładowy, w tym przypadku HOMO ligandów CO powinny być w stanie uczestniczyć w wiązaniach σ z metalem. W rzeczywistości nie jest to od razu oczywiste. Gdybyśmy wybrali ten sam układ współrzędnych metalu i ligandów, to oś wiązania CO, którą zdefiniowaliśmy jako oś z, nie wskazywałaby na metal i żadne nakładanie typu σ z orbitalami metalu nie mogłoby zajść. Dlatego musimy nadać każdemu ligandowi inny układ współrzędnych z osiami z skierowanymi w stronę metalu, jak na powyższym schemacie. Dopiero wtedy cząsteczka CO byłaby zorientowana tak, aby utworzyć wiązanie σ z metalem. Generalnie, konstruując MO, ligandy powinny być zawsze zorientowane w taki sposób aby umożliwić maksymalne nakładanie orbitali. Ponieważ mamy cztery ligandy, będziemy mieć cztery orbitale HOMO ligandów, które grupujemy i określamy typ symetrii znajdując, że orbitale HOMO czterech ligandów rozkładają się na dwie grupy: A₁ i T₂.

Możemy teraz skonstruować molekularny diagram orbitalny dla wiązania σ. Orbital 4s i jeden z orbitali grupy ligandów mają symetrię A₁, co po połączeniu daje wiążący orbital 1a₁ i orbital antywiążący 2a₁. Orbitale 4p i trzy orbitale d metalu mają typ symetrii T₂, tak jak trzy orbitale grupy ligandów. Daje to w sumie dziewięć orbitali, co oznacza, że musimy skonstruować dziewięć orbitali cząsteczkowych o symetrii t₂. Z powodu trójkrotnej degeneracji tych orbitali muszą istnieć trzy zestawy potrójnie zdegenerowanych orbitali cząsteczkowych. Możemy założyć, że jedna ich grupa będzie wiążąca, jedna w przybliżeniu niewiążąca, a jedna antywiążąca. Możemy je nazwać odpowiednio 1t₂, 2t₂ i 3t₂. 2t₂ ma właściwie charakter antywiążący. Pozostały nam orbitale metalu o symetrii e, które ze względu na symetrię nie oddziałują z orbitalami ligandów pozostając niewiążące. Pozostaje umiejscowienie elektronami orbitali cząsteczkowych. Orbitale HOMO ligandów są zapełnione, co daje 4 × 2 = 8 elektronów. Elektrony te lokalizują się na 1t₂ i 1a₁ co pokazuje istnienie czterech wiązań σ metal-ligand. Wszystkie elektrony d metalu, których może być do dziesięciu, musiałyby znaleźć się na orbitalu e i/lub t₂. Poziom e w tetraedrze to niewiążące orbitale d_z2 i d_x2-y2, a poziom 2t₂ jest słabo antywiążący o silnie zaznaczonym charakterze orbitali d metalu (d_xy, d_yz i d_xz). Możemy zatem powiedzieć, że poziomy e i 2t₂ są orbitalami metalu w tetraedrycznym polu ligandów. Różnica energii między orbitalami e i 2t₂ to energia stabilizacji pola ligandów tetraedru Δ_t.

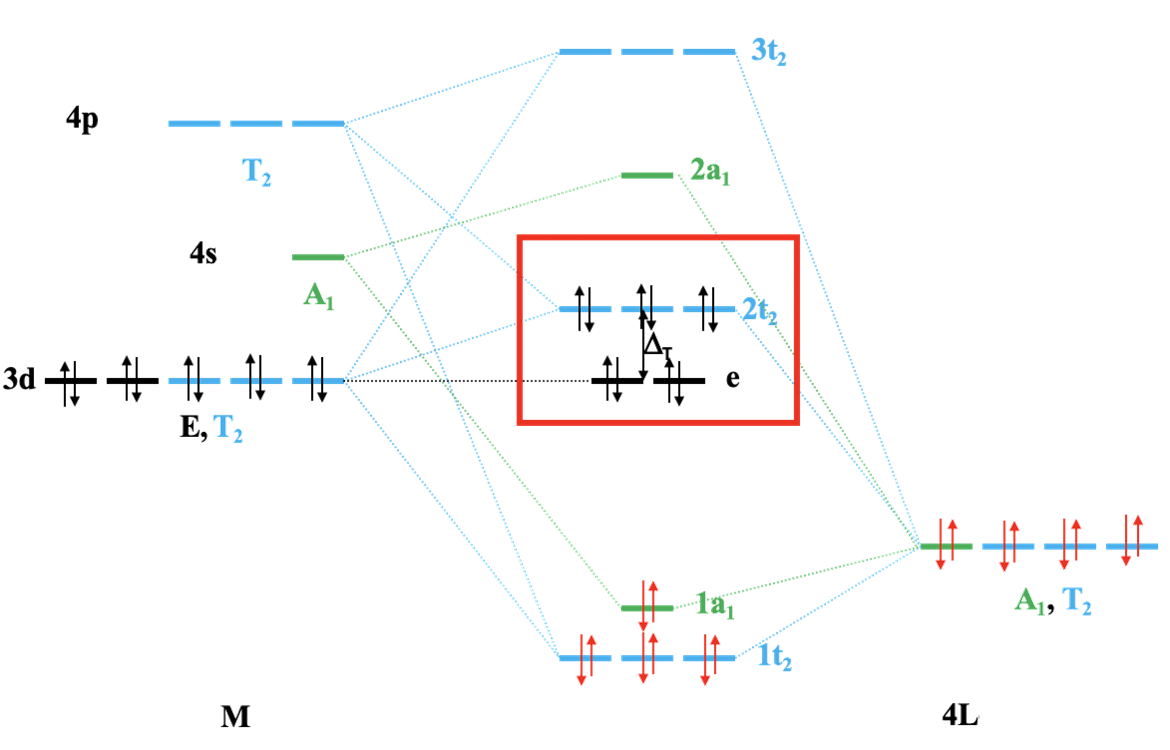Diagram MO odzwierciedlający wiązanie σ w tetraedrycznym kompleksie metalu przejściowego czwartego okresu

Wiązania π w kompleksie tetraedrycznym

Najpierw musimy zdecydować, czy istnieją orbitale ligandów, które są zorientowane tak, aby nakładały się na orbitale atomu metalu na sposób π. Widzimy, że żaden orbital liganda nie zachodzi na orbital d metalu dokładnie w sposób umożliwiający powstanie wiązania π, jednak orbitale e typu π metalu i 2e typu π^* ligandów nakładają się na siebie umożliwiając powstanie oddziaływania typu π. Z tego powodu możemy określić to oddziaływanie jako wiązanie π. Musimy jednak wziąć pod uwagę, że ze względu na mniejsze nakładanie się orbitali, wiązanie π w kompleksach tetraedrycznych jest słabsze niż w związkach o oktaedrycznym wielościanie koordynacyjnym. Ponieważ rozpatrujemy związek z CO jako ligandem, orbitali o symetrii π będzie cztery na każdy ligand, a zatem w sumie 4 × 4 = 16. Spośród nich będzie osiem orbitali wiążących e_π i osiem antywiążących e_π^*. Grupujemy orbitale wiążące i antywiążące, aby utworzyć dwa zestawy po osiem orbitali, i określamy ich symetrie. W każdej grupie orbitali ligandów mamy dwa orbitale typu E, trzy orbitale typu T₁ i trzy orbitale typu T₂. Ponieważ znamy teraz symetrię orbitali grup ligandów, możemy połączyć je z orbitalami metalu o tej samej symetrii w tetraedrycznym polu ligandów, tworząc orbitale cząsteczkowe typu π. Zróbmy to na przykładzie tetrakarbonylkuniklu(0). Użyjemy diagramu MO układu z wiązaniami σ jako punktu wyjścia i zmodyfikować go tak, aby uwzględniał wiązanie π. Dodając do diagramu nowe orbitale grupy ligandów bierzemy pod uwagę tylko e o symetrii E i T₂ pomijając T₁ ponieważ żaden orbital metalu nie ma symetrii t₁. Następnie musimy wziąć pod uwagę, że ligand CO jest silnym ligandem π-akceptorowym. Oznacza to, że należy brać pod uwagę tylko orbitale antywiążące π^* ligandów (LUMO cząsteczki CO).

Teraz łączymy orbitale typu π grupy ligandów i orbitale d metalu o tej samej symetrii, aby utworzyć orbitale cząsteczkowe typu π. Możemy połączyć orbitale ligandów typu e z niewiążącymi orbitalami typu e (d_z2 i d_x2-y2) metalu, tworząc parę wiążących MO i parę antywiążacych orbitali o symetrii e, która oznaczamy odpowiednio 1e i 2e. Teraz musimy zastanowić się nad wpływem orbitali  typu π grupy ligandów czyli T₂. Najpierw musimy zdać sobie sprawę, że mamy już trzy zestawy potrójnie zdegenerowanych orbitali cząsteczkowych t₂ powstałych w wyniku oddziaływania σ. Teraz oddziaływanie orbitali T₂ grupy ligandów z orbitalami cząsteczkowymi t₂ typu σ musi stworzyć inny zestaw potrójnie zdegenerowanych orbitali, tak aby całkowita liczba orbitali o symetrii t₂ pozostała taka sama. Oddziaływanie zachodzi głównie między cząsteczkowym 2t₂ i T₂ grupy ligandów, ponieważ energia poziomu 2t₂ jest zbliżona do energii orbitali T₂ ligandów. Prowadzi to do obniżenia energii 2t₂, w wyniku czego wcześniej słabo antywiążące orbitale stają się słabo wiążącymi. Dodatkowo powstają słabo antywiążące orbitale t₂. Możemy je nazwać 3t₂. Dawny orbital antywiążący 3t₂ oznaczymy jako 4t₂. Aby się upewnić czy poprawnie skonstruowaliśmy cząsteczkowe poziomy o symetrii t₂ sprawdzamy, czy liczba orbitali T₂ grupy ligandów, w tym σ i π, plus liczba orbitali T₂ metalu równa się liczbie orbitali cząsteczkowych t₂. Suma orbitali T₂ metalu + liczba orbitali o symetrii T₂ grupy ligandów wynosi 6 + 6 = 12. Liczba cząsteczkowych orbitali t₂ wynosi 4 × 3, czyli również 12.

Diagram MO tetraedrycznego kompleksu metalu przejściowego IV okresu (z ligandem π-akceptorowym)

Pozostaje wypełnienie poziomów elektronami. Orbitale π grupy ligandów, jako LUMO, są puste, a zatem ligand nie wnosi żadnych elektronów do wiązania π. Nikiel  jest na zerowym stopniu utlenienia, a zatem wnosi 10 elektronów. Konfiguracja elektronowa atomu Ni(0) to 3d ⁸4s ². Poziomy 1t₁ i 1a₁ są już zapełnione elektronami ligandów co wynika z wiązania σ. Zatem elektrony metalu znaleźć się na orbitalach cząsteczkowych 2e i 2t₂. Zarówno orbitale e, jak i 2t₂ są wiążące, a zatem możemy stwierdzić, że elektrony d metalu doznały stabilizacji w wyniku π-akceptorowych właściwości liganda. Widzimy tutaj analogię do oktaedrycznego pola ligandów. Podobnie jak w oktaedrycznym polu ligandów, ligandy π-akceptorowe mają tendencję do obniżania energii elektronów d metalu. Podobnie parametr rozszczepienia Δ_t rośnie w tetraedrycznym polu ligandów π-akceptorowych. Jednak wzrost jest znacznie mniejszy w porównaniu z polem oktaedrycznym. Dzieje się tak dlatego, że w oktaedrycznym polu ligandów energia poziomu e_g nie zmienia się w wyniku odziaływania π-akceptorowego, a jedynie energia orbitali t_2g ulega obniżeniu. W przypadku tetraedrycznego pola ligandów obniża się zarówno energia orbitali e, jak i t₂, przy czym energia poziomu e ulega tylko nieznacznie większemu obniżeniu niż energia orbitali t₂. Fakt ten może również służyć jako dodatkowe wyjaśnienie, dlaczego kompleksy tetraedryczne nigdy nie tworzą kompleksów niskospinowych, nawet z ligandami o silnie zaznaczonych właściwościach  π-akceptorowych. Wpływ liganda na wartość Δ_t jest zbyt mały, ponieważ zarówno energia orbitali e, jak i t₂ ulega obniżeniu.

Diagram MO tetraedrycznego kompleksu metalu przejściowego IV okresu (π-donor)

Zastanówmy się teraz, jak ligand będący π-donorem wpływa na wielkość parametru rozszczepienia Δ_t. W tym przypadku musimy tylko wziąć pod uwagę wiążące orbitale ligandów o symetrii E i T₂, jeśli ligand tworzy wiązania π. Te orbitale będą energetycznie znajdować się poniżej orbitali grupy ligandów tworzących wiązanie σ. Jeśli ligand jest prostym jonem, takim jak Cl^–, rozważymy orbitale grupy ligandów składające się z zapełnionych orbitali p o symetrii odpowiedniej do nakładania się typu π z orbitalami metalu. Orbitale grupy ligandów miałyby zasadniczo taką samą energię jak orbitale σ LGO. Skonstruujmy diagram MO TiCl₄, czyli dla układu z ligandami chlorkowymi jako typowymi ligandami π-donorowymi. Ponownie zaczniemy od diagramu MO obejmującego tylko wiązania σ, a następnie go zmodyfikujemy. Orbitale grupy ligandów E będą teraz oddziaływać z orbitalami e metalu. Ta interakcja prowadzi do pary wiążących i pary antywiążących MO o symetrii e. Oznacza to, że efektywnie, niewiążące orbitale e metalu stają się antywiążącymi i przemieszczają się w górę na skali energii. Dodatkowy poziom wiążący e musi mieć mniejszą energię niż orbitale π grupy ligandów o symetrii E. Oddziałyanie orbitali o symetrii T₂ grupy ligandów z orbitalami t₂ metalu tworzy dodatkowy zestaw wiążących orbitali t₂. Energia orbitali 2t₂ rośnie i stają się one w konsekwencji bardziej antywiążące. Teraz wprowadzamy elektrony na orbitale cząsteczkowe. Orbitale typu π grupy ligandów mają w sumie osiem elektronów. Te elektrony trafią do nowo utworzonych orbitali cząsteczkowych wiążących 1e i 1t₂, c prowadzi do ich stabilizacji. Tytan w TiCl₄ jest na +4 stopniu utlenienia, więc formalnie mamy tutaj konfigurację d⁰, czyli metal nie dostarcza elektronów. To wyjaśnia stabilność TiCl₄, który nie spełnia reguły 18 elektronów. Mamy tylko 8 elektronów, ale wszystkie wiążące orbitale cząsteczkowe są zapełnione elektronami, a wszystkie pozostałe są puste. Gdyby atom Ti miał elektrony d, musiałby znaleźć się na orbitalach 2e i 3t₂, które są antywiążące, co zdestabilizowałoby cząsteczkę związku. Ogólnie ligandy będące donorami π zwiększają energię elektronów d metalu i jest to kolejna analogia do oktaedrycznego pola ligandów. Zastanówmy się jaki jest wpływ liganda π-donorowego na wartość parametru rozszczepienia Δ_t. Energie orbitali granicznych metalu, e i t₂, wzrosły, ale energia poziomy e wzrosła bardziej niż poziomu t₂. Oznacza to, że Δ_t ogólnie zmalało, czyli ligandy π-donorowe prowadzą do zmniejszenia parametru rozszczepienia.

Planarne kompleksy kwadratowe

Jako ostatni przykład omówimy teraz molekularny diagram orbitalny kwadratowego kompleksu płaskiego. Będzie to najbardziej skomplikowany diagram MO, jaki omówimy. Większa złożoność wynika z niższej symetrii związku, który należy do grupy punktowej D_4h, natomiast kompleksy tetra– i oktaedryczne należą do grup punktowych o wysokiej symetrii T_d i O_h.

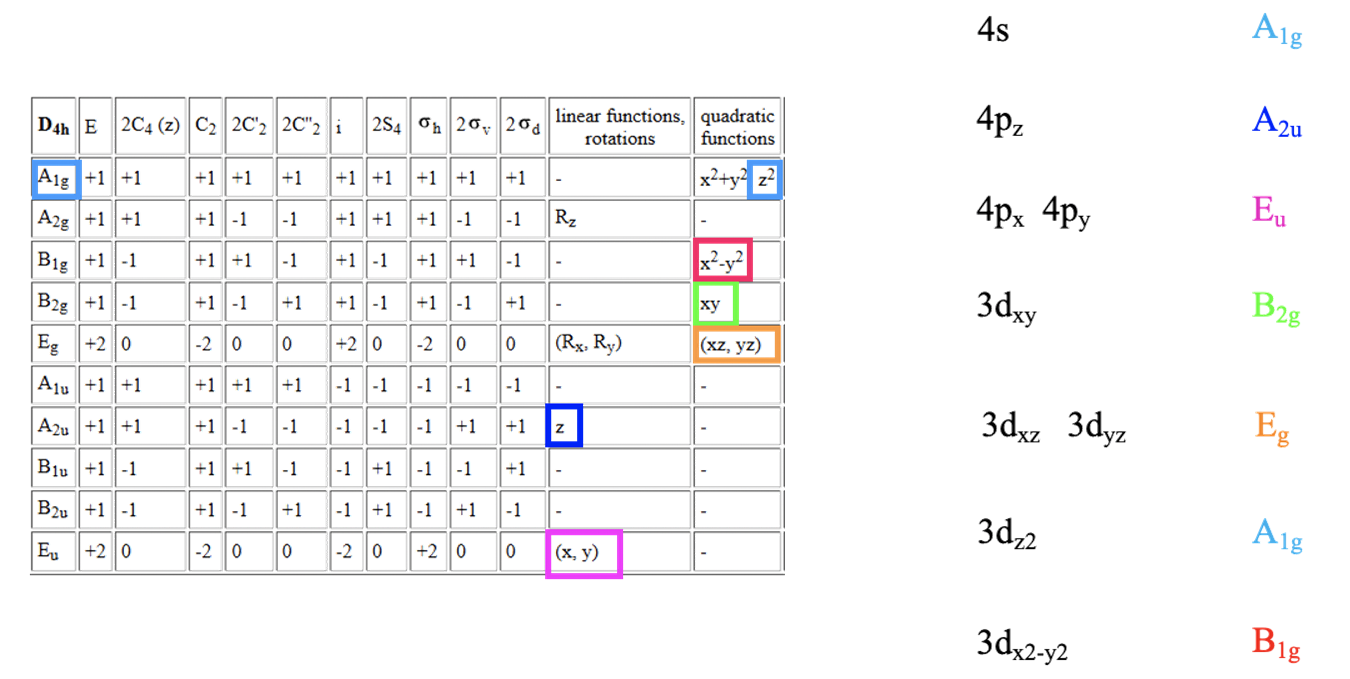Tabela charakterów dla grupy punktowej D4h i symetria orbitali metalu.

Niższa symetria prowadzi do większego zniesienia degeneracji orbitali cząsteczkowych. Na początek zdefiniujmy osie układu współrzędnych. Rozsądnie byłoby zdefiniować płaszczyznę xy jako płaszczyznę cząsteczki ze współrzędnymi x i y przechodzącymi przez wiązania. Oś z byłaby prostopadła do płaszczyzny cząsteczki. Zakładając, że mamy kompleks metalu przejściowego czwartego okresu, orbitale 3d, 4s i 4p są orbitalami granicznymi. Tabela charakterów grupy punktowej D_4h pokazuje, że symetria orbitalu 4s to A_1g, orbitali 4p to A_2u dla orbitalu 4p_z i e_u dla 4p_x i 4p_y. Orbitale d mają typy symetrii A_1g, B_1g, B_2g i E_g odpowiednio dla 3d_z2, d_x2-y2, 3d_xy i 3d_xz, 3d_yz.

Diagram orbitali cząsteczkowych jonu CN–

W kolejnym kroku określamy poziomy HOMO ligandów zdolne tworzyć wiązania σ. Nie istnieją kwadratowe planarne kompleksy karbonylowe, dlatego zamiast CO użyjemy liganda cyjanowego. Ligand cyjanowy jest izoelektronowy z ligandem karbonylowym, ale  ponieważ azot ma o jeden elektron mniej niż O, musimy dodać jeden elektron do liganda cyjanowego tworząc anion CN^–. Liczba, symetria i kolejność energii MO dla CN^– i CO są takie same. Dlatego ligand cyjanowy ma orbitale HOMO odpowiednie do utworzenia wiązania σ i możemy je użyć do budowy wiązań cząsteczkowych σ. Każdy ligand ma jedno HOMO, dlatego mamy w sumie cztery HOMO, które wykazują symetrię: Γ_σ =A_1g + E_u + B_1g. mamy zatem orbital grupy ligandów o symetrii A_1g, dwa o symetrii E_u i jeden o symetrii B_1g. Mamy teraz wszystkie informacje niezbędne do skonstruowania diagramu orbitali cząsteczkowych dla związku z wiązaniami σ. Orbitale 4s i 3d_z2 mają typ symetrii A1g, taki sam jak jeden z orbitali grupy ligandów. Otrzymamy zatem trzy orbitale cząsteczkowe tego typu symetrii, jeden wiążący, jeden niewiążący i jeden antywiążący, oznaczymy je odpowiednio 1a_1g, 2a_1g i 3a_1g. Symetrię B_1g mają orbital 3d_x2-y2 i jeden z orbitali grupy ligandów, a zatem ich kombinacja utworzy cząsteczkowy orbital wiążący i  antywiążący. Orbitale 4p_x i 4p_y mają symetrię E_u, jak pozostałe dwa orbitale grupy ligandów. W wyniku kombinacji otrzymujemy dwa dwukrotnie zdegenerowane wiążące i dwa antywiążące orbitale cząsteczkowe o symetrii e_u. Pozostały nam orbitale d_xy, d_xz i d_yz o symetrii odpowiednio B_2g i E_g. Ponadto mamy orbital p_z metalu o symetrii a_2u. Te orbitale metalu nie mają odpowiedników co do symetrii wśród orbitali grupy ligandów. Dlatego pozostają jako  niewiążące na diagramie MO. Wypełnijmy elektronami orbitale cząsteczkowe. Orbitale HOMO ligandów są zajęte przez elektrony, a ponieważ mamy cztery ligandy, musimy wziąć pod uwagę osiem elektronów. Elektrony te będą wypełniać orbitale cząsteczkowe 1_a1, 1b_1g i 1e_u. Wszystkie te orbitale są wiążące. Zatem teoria pola ligandów jest w stanie wyjaśnić cztery wiązania i kwadratowy płaski kształt cząsteczki. Pora na elektrony jonu centralnego. Możemy mieć do dziesięciu elektronów d, w zależności od jonu metalu, a te dziesięć elektronów zajmie niewiążące orbitale b_2g i e_g oraz niewiążący orbital 2a_1g i antywiążący 2b_1g. Te orbitale możemy rozpatrywać jako orbitale metalu w kwadratowym płaskim polu ligandów. Orbital b_2g to d_xy w kwadratowym planarnym polu ligandów, e_g to d_xz i d_yz, poziom 2a_1g to d_z2, a 2b_1g to d_x2-y2. W teorii pola krystalicznego największą energię miał orbital d_x2-y2. Orbital d_z2 miał mniejszą energię niż d_xy, który nie był zdegenerowany z orbitalami d_xz i d_yz. Różnica wynika z faktu, że w teorii pola ligandów orbital d_xy jest uważany za niewiążący, w ogóle nie oddziałujący z ligandami, podczas gdy w teorii pola krystalicznego zakłada się silne odpychanie elektrostatyczne między d_xy a ligandami, ponieważ orbital d_xy znajduje się w płaszczyźnie cząsteczki.

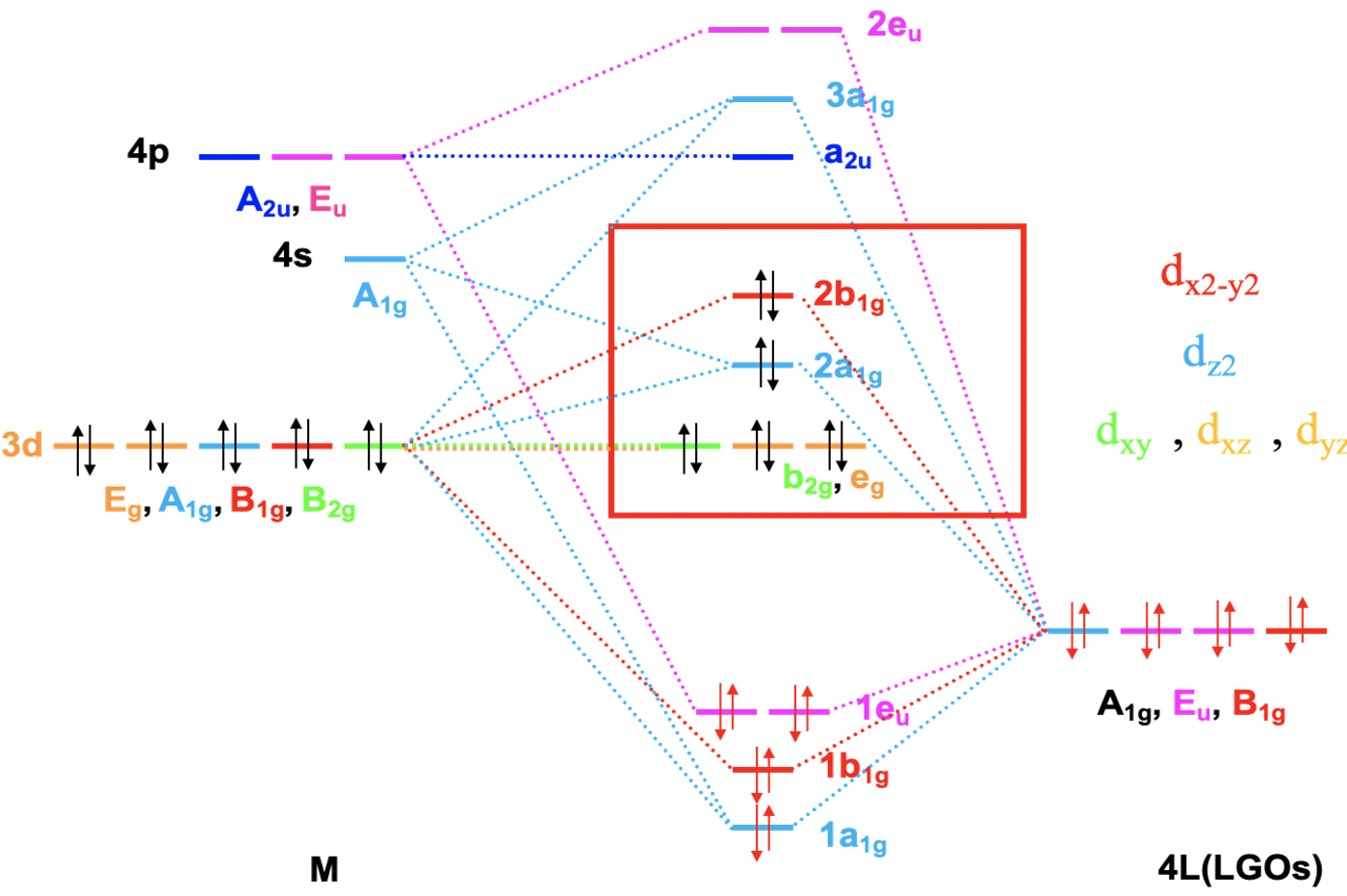Diagram MO dla kwadratowego płaskiego kompleksu metali przejściowych czwartego okresu (wiązania σ)

Przyjrzyjmy się teraz wiązaniu π w kwadratowym płaskim kompleksie metalu przejściowego. Dla liganda CN^– orbitale, które mają odpowiednią symetrię, aby nakładać się z orbitalami metalu tworząc wiązanie π to orbitale 1e i 2e (π i π^*)  na diagramie MO dla CO. Ponieważ mamy cztery ligandy, w sumie mamy osiem orbitali π i osiem π^*. Teraz musimy wziąć pod uwagę, że cztery z orbitali π znajdują się w płaszczyźnie xy, podczas gdy pozostałe cztery znajdują się powyżej i poniżej płaszczyzny xy. Te pierwsze nazywamy orbitalami równoległymi, a drugie prostopadłymi, ponieważ są zorientowane odpowiednio równolegle i prostopadle do płaszczyzny xy. Musimy je rozróżnić, ponieważ mają inną symetrię i inaczej nakładają się z orbitalami d metalu. Analogicznie zachowują się orbitale antywiążące. Zgrupujemy orbitale, aby utworzyć cztery zestawy orbitali ligandów π⊥, π||, π^*⊥ i π^*||. Naszym następnym zadaniem jest określenie typów symetrii tych orbitali. Zarówno π⊥, jak i π^*⊥ zawierają jeden orbital o symetrii A_2u, dwa E_g i jeden B_2u; π|| i π^*|| przekształcają się jako jeden A_2g, dwa E_u i jeden B_2g.

Teraz musimy wprowadzić orbitale cząsteczkowe π do diagramu uwzględniającego jedynie wiązania σ. Po pierwsze, musimy rozważyć, które z orbitali π ligandów mają odpowiednią symetrię do kombinacji z orbitalami d metalu.

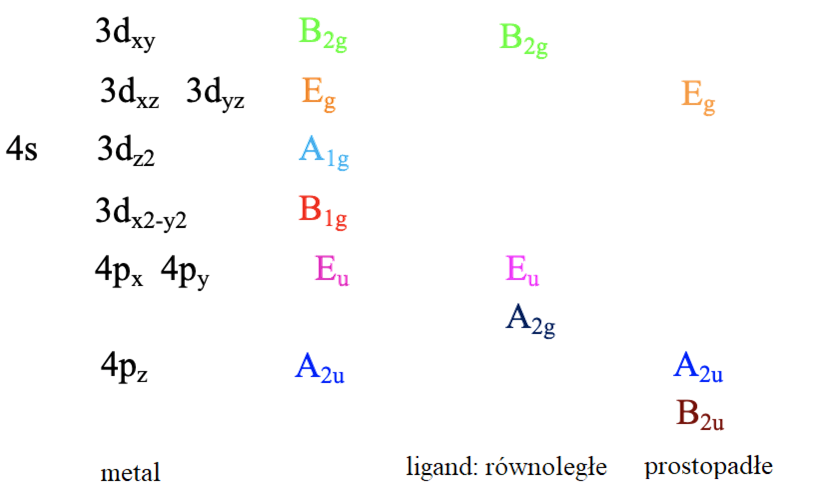Typy symetrii orbitali granicznych metalu, oraz orbitali ligandów zdolnych do tworzenia wiązań π

Widzimy, że wśród orbitali ligandów leżących w płaszczyźnie xy tylko A_1g i B_1g, a wśród prostopadłych do płaszczyzny xy tylko orbitale E_g mają odpowiednią symetrię. Dlatego bierzemy pod uwagę tylko A_1g, B_1g i E_g grupy ligandów. W celu uzyskania właściwego diagram dla kwadratowego kompleksu z ligandami cyjanowymi, konieczne jest rozważenie oddziaływania orbitali 4s i 4p z orbitalami π ligandów. Orbital 4s przekształca się jako A_1g, a 4p jako A_2u i E_u.

Skonstruujmy teraz diagram MO dla kompleksu o symetrii D_4h z ligandami cyjanowymi, biorąc pod uwagę zarówno wiązania σ, jak i π na przykładzie anionu kompleksowego [Ni(CN)₄]^2–.  Ze względu na złożoność diagramu nie będziemy modyfikować diagramu MO dla wiązania σ, jak to zrobiliśmy wcześniej, ale skonstruujemy kompletny diagram od podstaw. W przypadku kompleksu [Ni(CN)₄]^2– orbitale σ grupy ligandów są energetycznie umiejscowione poniżej orbitali d niklu, orbitale  π ligandów mają mniej więcej taką samą energię jak orbitale d, a antywiążące orbitale π^* ligandów mają energię znacznie wyższa niż orbitale 4p niklu. Widzimy, że jest tylko jeden orbital σ ligandów, o symetrii A_1g, może kombinować z 4s i 3d_z2, które również mają ten sam typ symetrii. Prowadzi to do utworzenia poziomów wiążącego, nie wiążącego i antywiążącego a_1g, które możemy oznaczyć odpowiednio 1a_1g, 2a_1g i 3a_1g. Następnie weźmy pod uwagę orbitale B_2g. Jest jeden orbital d o takiej symetrii, i dwa orbitale grupy ligandów (LGO). Oddziaływanie zachodzi praktycznie tylko z wiążącym orbitalem B_2g ligandów ponieważ energie d_xy i orbitalu wiążącego ligandów są podobne. Prowadzi to do cząsteczkowego orbitalu wiążącego i anty wiążącego typu π o symetrii B_2g. Energia antywiążącego orbitalu o symetrii B_2g ligandów jest zbyt duża aby w znaczący sposób oddziaływać z orbitalem d_xy metalu. Dlatego pozostaje na diagramie z niemal niezmienioną energią. Przejdźmy teraz do orbitali B_1g. Mamy orbital d_x2-y2 o symetrii B_1g i orbital  σ ligandów o symetrii B_1g. Daje to wiążący i antywiążący orbital  cząsteczkowy o symetrii B_1g. Dalej rozpatrujemy orbitale E_g. Istnieją dwa orbitale d, dwa π i dwa π^* ligandów o tej symetrii. Ponownie, π^* ligandów mają zbyt dużą energię, tak że oddziaływanie występuje głównie między d_xz, d_yz metalu a π ligandów. Prowadzi to do pary wiążących i pary antywiążących orbitali cząsteczkowych; π^* ligandów pozostawiamy z niezmienioną energią. Orbitale 4p metalu mają typy symetrii, których jeszcze nie rozważaliśmy: A_2u i E_u. Zacznijmy od orbitali E_u. Istnieją dwa orbitale σ,  dwa π i dwa π^* ligandów o symetrii E_u. Ogólnie mamy cztery pary orbitali o tej symetrii i spodziewamy się czterech par orbitali cząsteczkowych o symetrii E_u. Możemy przyjąć, że będą to poziomy wiążący, słabo wiążący, słabo antywiążący i silnie antywiążący. Możemy je nazwać odpowiednio 1e_u, 2e_u, 3e_u i 4e_u. 4e_u ma prawie wyłącznie charakter antywiążącego orbitalu π^* -E_U ligandów ze względu na energię. Przejdźmy teraz do orbitali A_2u: istnieją orbitale π i π^* ligandów o symetrii A_2u, które mogą kombinować z orbitalami 4p o symetrii A_2u. Prowadzi to ogólnie do trzech MO A_2u, jednego wiążącego, jednego w przybliżeniu niewiążącego i jednego antywiążącego wiązaniu. Wykorzystaliśmy wszystkie orbitale d metalu. Zauważamy, że nadal istnieją pewne niewykorzystane orbitale ligandów, są to π i π^* o symetrii A_2g oraz B_2u, pozostają one niewiążące.

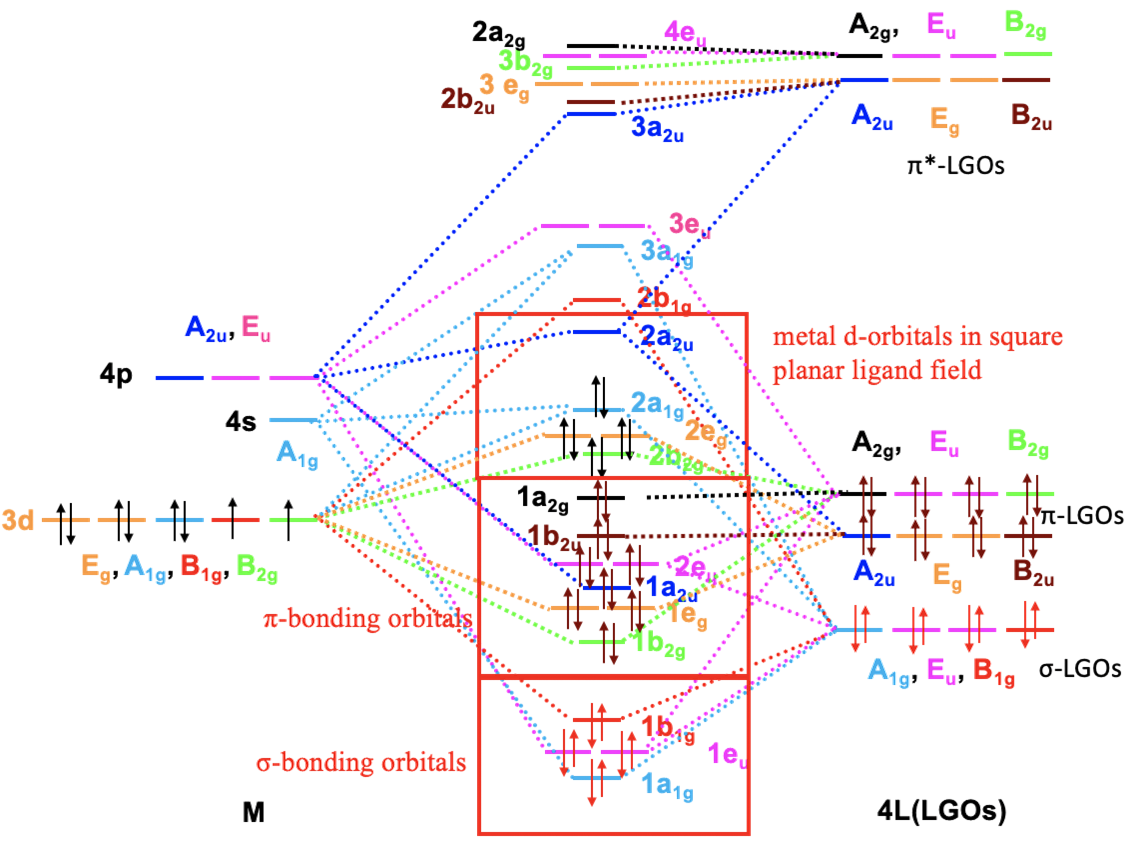Diagram OM kompleksu płaskokwadratowego z ligandami cyjanowymi z uwzględnieniem wiązania π.

Teraz musimy wypełnić diagram elektronami. Po pierwsze, należy wziąć pod uwagę elektrony σ. W sumie jest osiem elektronów pochodzących z czterech zajętych orbitali σ ligandów. Umieszczamy je na orbitalach cząsteczkowych o najniższej energii, czyli 1a₁, 1e_u i 1b₁. W ten sposób mamy cztery wiązania σ w cząsteczce kompleksu (blok wiązań σ). Następnie musimy rozważyć elektrony π ligandów. W sumie jest osiem takich orbitali zawierających 16 elektronów. Umieszczamy je na diagramie na kolejnych orbitalach 1b_2g, 1e_g, 1a_2u, 2e_u, 1b_2u i 1a_2g. Orbitale te są albo wiążące, albo niewiążące, a zatem ogólnie elektrony π liganda ulegają stabilizacji dzięki oddziaływaniom π metal–ligand. Pozostają nam elektrony d metalu. Konfiguracja jonu Ni²⁺ to d ⁸, te elektrony trafiają na orbitale 2b_2g, 2e_g i 2a_1g, które są albo niewiążące, albo antywiążące. Oznacza to, że elektrony metalu są ogólnie zdestabilizowane. Takie zachowanie jest zgodne z charakterem liganda cyjanowego będącym donorem π. Wyjaśnia to również fakt, że planarne kompleksy kwadratowe są najczęściej 16– a nie 18–elektronowe. Gdybyśmy mieli jeszcze dwa elektrony, musiałyby one znaleźć się na znacznie wyżej energetycznym orbitalu 2a_2u. Różnica energii między orbitalami 2a_2u i 2a_1g jest znacznie większa niż między orbitalami 1a_1g, 2b_2g i 2e_g. Ogólnie rzecz biorąc, możemy nazwać orbitale 2a_u, 2a_1g, 2e_g i 2b_g rozszczepionymi orbitalami d w kwadratowym płaskim polu ligandów. W takim polu ligandów mamy trzy parametry rozszczepienia ∆. ∆₃ to różnica energii orbitali 2b_2g i 2e_g, ∆₂ to różnica energii orbitali 2e_g i 2a_1g, a ∆₁ to różnica energii orbitali 2a_1g i 2a_2u. ∆₁ jest znacznie większe niż pozostałe dwa parametry rozszczepienia. Jest również prawie zawsze większa niż energia sparowania spinów, dlatego planarne kompleksy kwadratowe są prawie zawsze kompleksami niskospinowymi. Ogólnie widzimy, że diagram MO może stać się bardzo złożony, nawet dla stosunkowo prostej cząsteczki o stosunkowo wysokiej symetrii.