 Principles of Chemistry
Principles of Chemistry
- > Home
-
>
Historia chemii
- > Początki chemii
- > Rozwój alchemii
- > Jatrochemia
- > Badanie spalania i powietrza
- > Odkrycie i badanie gazów
- > Powstanie nowoczesnej chemii
- > Prawa chemiczne
- > Narodziny teorii atomowej
- > Elektrochemia
- > Berzelius, Hisinger, Faraday
- > Początki chemii organicznej
- > Substytucja
- > Wartościowość
- > Chemia fizyczna
- > Rozwój chemii nieorganicznej
- > Struktura atomu
-
>
Pierwiastki
- > Starożytność
- > Średniowiecze
- > Powietrze i woda
- > Analiza chemiczna
- > Halogeny
- > Elektrochemia
- > Metody spektroskopowe
- > Pierwiastki ziem rzadkich
- > Gazy szlachetne
- > Pierwiastki radioaktywne
- > Szeregi pierwiastków promieniotwórczych
- > Pierwiastki otrzymane sztucznie
- > Pierwiastki transuranowe
- > Podsumowanie
- > Układ okresowy
-
>
Mechanika falowa
- > Podstawy teoretyczne
- > Moment pędu
- > Równanie Schrodingera
- > Oscylator liniowy
- > Pole o symetrii sferycznej i pole kulombowskie
- > Spin
- > Identyczność cząstek
- > Oddziaływanie wymienne
- > Druga kwantyzacja
- > Poziomy energetyczne atomów
- > Układ okresowy
- > Atom w polu elektrycznym
- > Atom w polu magnetycznym
- > Cząsteczka dwuatomowa
- > Orto- i parawodór
- > Teoria relatywistyczna
- > Kwantowanie pola elektromagnetycznego
- > Fotony
- > Równanie Diraca
- > Cząstki i antycząstki
- > Atom i cząsteczka
-
>
Związki metali przejściowych
- > Powłoka walencyjna metali przejściowych
- > Efekt Jahna-Tellera
- > Teoria pola krystalicznego
- > Teoria pola ligandów
- > Widma elektronowe
- > Wiązania metal-metal
- > Własności magnetyczne
- > Trwałość związków koordynacyjnych
- > Związki z ligandami π–akceptorowymi
- > Arenowe związki koordynacyjne
- > Oddziaływania agostyczne
- > Wiązania chemiczne
- > Pojęcia chemii nieorganicznej
- > Mechanizmy reakcji
- > Oddziaływania międzycząsteczkowe
- > Elementy fizyki
- > Chemia organiczna
 Właściwości magnetyczne związków koordynacyjnych
Właściwości magnetyczne związków koordynacyjnych
Jedną z właściwości związków koordynacyjnych metali przejściowych związaną z obecnością niesparowanych elektronów jest ich magnetyzm. Paramagnetyzm jonów metali wynika z obecności orbitalnego i spinowego momentu magnetycznego niesparowanych elektronów. Koordynowanie jonu metalu powoduje częściowe wygaszenie momentu orbitalnego przez co własności paramagnetyczne związku koordynacyjnego w przybliżeniu są zależne od momentu spinowego niesparowanych elektronów. W związku z tym pomiar podatności magnetycznej związku koordynacyjnego w pierwszej kolejności pozwala określić ilość niesparowanych elektronów, a tym samym jego stan spinowy.
Jeżeli dana substancja znajdzie się w polu magnetycznym o natężeniu H to pojawia się indukcja magnetyczna B wyrażona wzorem:
B =H + 4πI
gdzie czynnik 4πI jest związany bezpośrednio z właściwościami substancji umieszczonej w polu magnetycznym, I oznacza w szczególności moment magnetyczny na jednostkę objętości substancji. Podzielenie tego równania przez H prowadzi do zależności:
P =1 + 4πκ
gdzie P oraz κ oznaczają odpowiednio przenikalność i podatność magnetyczną na jednostkę objętości substancji niezależne od rozmiaru próbki. W praktyce bardziej wygodnym jest posługiwanie się podatnością wyrażaną na jednostkę masy (gram) niż jednostkę objętości:
χ = κ /d, gdzie d oznacza gęstość substancji. Można oczywiście wyrazić podatność w formie podatności molowej przez przemnożenie podatności gramowej przez masę molową substancji (χM=χ•masa molowa).
Wyrażenie na przenikalność magnetyczną, podane powyżej, prowadzi do fundamentalnego podziału substancji. Otóż jeżeli wartość przenikalności P jest mniejsza od jedności, czyli P < 1, a tym samym I, κ i χ są ujemne, mamy do czynienia z substancją diamagnetyczną. Mówiąc obrazowo, substancja diamagnetyczna w magnetycznym polu niejednorodnym zajmuje miejsce o najniższym natężeniu pola magnetycznego. Dla substancji diamagnetycznych wyznaczone eksperymentalnie wartości podatności magnetycznych charakteryzują się bardzo małymi wielkościami ze znakiem ujemnym. Dodatkowo praktycznie nie wykazują zależności od siły pola magnetycznego i temperatury. O substancjach, dla których wartość przenikalności jest większa od jedności, a moment magnetyczny i podatność przyjmują dodatnie wartości mówimy jako o paramagnetykach. Eksperymentalne wartości podatności magnetycznej są z reguły większe niż w przypadku diamagnetyków (oczywiście chodzi o wartości bezwzględne), a dodatkowo występuje zależność od siły pola magnetycznego i temperatury. W obrębie substancji paramagnetycznych mamy jeszcze dwie podgrupy, czyli substancje wykazujące ferromagnetyzm i antyferromagnetyzm. Te dwa zjawiska są związane nie z pojedynczymi cząsteczkami, a z oddziaływaniem centrów paramagnetycznych w całym krysztale. Wartości podatności magnetycznej dla tego typu związków są bardzo wysokie, jednak tego typu odziaływań nie należy oczekiwać w przypadku związków koordynacyjnych, chociaż niektóre tlenki czy fluorki wykazują cechy ferro- lub antyferromagnetyczne. Z drugiej strony zjawisko porządkowania momentów magnetycznych w związkach koordynacyjnych jest spotykane.
W przypadku paramagnetyzmu występuje zależność podatności magnetycznej od temperatury, którą wyraża prawo Curie-Weissa:
![]() gdzie θ jest wielkością stałą o wymiarze temperatury. Jak widać, jeżeli prawo Curie-Weissa jest spełnione to wykres zależności odwrotności podatności magnetycznej od temperatury jest linią prostą odcinającą na osi temperatury wartość –θ. Dodatkowym elementem, który należy uwzględnić przy rozpatrywaniu paramagnetyzmu związków koordynacyjnych jest udział diamagnetycznych ligandów w podatności magnetycznej próbki. W takim przypadku wartość podatności magnetycznej można wyrazić wzorem:
gdzie θ jest wielkością stałą o wymiarze temperatury. Jak widać, jeżeli prawo Curie-Weissa jest spełnione to wykres zależności odwrotności podatności magnetycznej od temperatury jest linią prostą odcinającą na osi temperatury wartość –θ. Dodatkowym elementem, który należy uwzględnić przy rozpatrywaniu paramagnetyzmu związków koordynacyjnych jest udział diamagnetycznych ligandów w podatności magnetycznej próbki. W takim przypadku wartość podatności magnetycznej można wyrazić wzorem:
![]()
| kation | anion | ligandy obojętne i aniony organiczne | |||
| Li+ | –1,0 | F– | –9,1 | H2O | –13 |
| Na+ | –6,8 | Cl– | –23,4 | CO | –10 |
| K+ | –14,9 | Br– | –34,6 | etylenodiamina | –46 |
| Rb+ | –22,5 | I– | –50,6 | fenantrolina | –128 |
| Cs+ | –35,0 | CN– | –13,0 | CH3COO– | –30 |
| NH4+ | –13,3 | NCS– | –31,0 | C2O42– (szczawian) | –25 |
| Mg2+ | –5,0 | CO32– | –28,0 | C5H5– (cyklopentadienyl) | s–65 |
| Ca2+ | –10,4 | ClO4– | –32,0 | NH3 | –18 |
| Zn2+ | –15,0 | NO2– | –10,0 | C2H4 | –15 |
| Hg2+ | –40,0 | NO3– | –18,9 | pirydyna | –49 |
| OH– | –12,0 | bipirydyl | –105 | ||
| O2– | –7,0 | mocznik | –34 | ||
| SO42– | –40,1 | tiomocznik | –42 | ||
| HSO4– | –35,0 | acetyloacetonian | –52 |
Zakładając addytywność przyczynków diamagnetycznych należy pamiętać, że ich wartość nie musi być stała, niezależna od rodzaju związku chemicznego, i może ulegać zmianie. Jest to zrozumiałe biorąc pod uwagę choćby taki czynnik jak polaryzowalność jonów, zmieniająca się w zależności od otoczenia, co wpływa na udział diamagnetyzmu w podatności magnetycznej próbki.
Poprawkę diamagnetyczną można obliczyć z zależności Pascala:
![]() którym nA oznacza liczbę atomów lub jonów, χA ich podatność magnetyczną (stałą Pascala), a Σλ sumę poprawek strukturalnych takich jak na przykład rola wiązań.
którym nA oznacza liczbę atomów lub jonów, χA ich podatność magnetyczną (stałą Pascala), a Σλ sumę poprawek strukturalnych takich jak na przykład rola wiązań.
| χA | |||
| H | –2,93 | F | –6,3 |
| C | –6,00 | Cl | –20,1 |
| N | –5,57 | Br | –30,6 |
| N (w pierścieniu) | –4,61 | I | –44,6 |
| N (amid) | –1,54 | S | –15,0 |
| N (diamid, imid) | –2,11 | P | –26,3 |
| O | –4,61 | As(III) | –20,9 |
| O (keton) | +1,73 | As(V) | –43.0 |
| O2 (kwas karboksylowy) | –7,95 | Sb(III) | –74,0 |
| λ | |||
| C (pierścień benzenowy) | –0,24 | C≡C | +0,8 |
| C (na złączeniu dwóch pierścieni) | –3,07 | C=N | +8,15 |
| C–Cl | +3,10 | C≡N | +0,8 |
| C–Br | +4,10 | C=N–R | +8,20 |
| C=C (wiązanie) | +5,5 | N=N | +1,8 |
| C=C–C=C | +10,0 | N=O | +1,7 |
Rozpatrując pojedynczy elektron, w uproszczonym modelu (poruszający się po orbicie kołowej) łatwo zauważyć, że musi mu towarzyszyć pewne pole magnetyczne prostopadłe do płaszczyzny ruchu elektronu. Wartość momentu magnetycznego elektronu w takim ujęciu można wyrazić w postaci:
 gdzie e – ładunek elektronu; ω prędkość kątowa, r promień orbity. W ujęciu mechaniki kwantowej licznik powyższego wyrażenia jest związany z orbitalną liczbą kwantową, w związku z czym możemy zapisać:
gdzie e – ładunek elektronu; ω prędkość kątowa, r promień orbity. W ujęciu mechaniki kwantowej licznik powyższego wyrażenia jest związany z orbitalną liczbą kwantową, w związku z czym możemy zapisać:
![]() gdzie
gdzie
 to magneton Bohra, wartość stała równa 9,274•10–24 J•T-1 (9,274•10–21 erg•Oe–1). Ponieważ elektron posiada, poza momentem orbitalnym, spin (moment kątowy) zatem moment magnetyczny elektronu jest również zależny od jego spinu:
to magneton Bohra, wartość stała równa 9,274•10–24 J•T-1 (9,274•10–21 erg•Oe–1). Ponieważ elektron posiada, poza momentem orbitalnym, spin (moment kątowy) zatem moment magnetyczny elektronu jest również zależny od jego spinu:
![]()
Momenty orbitalne i spinowe ulegają sprzężeniu, które powoduje pojawienie się wartości wypadkowej j (liczby kwantowej J w przypadku atomów  wieloelektronowych), a tym samym wypadkowy moment magnetyczny nie jest zgodny tylko z momentem kątowym. Sytuacja ta jest zilustrowana na rysunku. Jak widać sprzężenie Russela-Sandersa (LS) powoduje pojawienie się momentu zależnego od wypadkowej wartości J, ale szybka precesja wektorów momentów orbitalnego i spinowego wokół wektora J wpływa na wartość wypadkowego momentu magnetycznego w ten sposób, że jego wartość odpowiada długości odcinka AC na rysunku, a nie długości wektora μJ.
wieloelektronowych), a tym samym wypadkowy moment magnetyczny nie jest zgodny tylko z momentem kątowym. Sytuacja ta jest zilustrowana na rysunku. Jak widać sprzężenie Russela-Sandersa (LS) powoduje pojawienie się momentu zależnego od wypadkowej wartości J, ale szybka precesja wektorów momentów orbitalnego i spinowego wokół wektora J wpływa na wartość wypadkowego momentu magnetycznego w ten sposób, że jego wartość odpowiada długości odcinka AC na rysunku, a nie długości wektora μJ.
Szybkość precesji jest tak duża, że dostatecznym przybliżeniem jest przyjęcie wartości długości promienia BC na rysunku za równą zero, a tym samym wyrażenie na moment magnetyczny przybiera postać:
![]() Czynnik g, czyli czynnik Landégo lub żyromagnetyczny wynika z relatywistycznej mechaniki kwantowej, i w ogólności można go związać z różnicami w rozkładzie masy i ładunku w elektronie. Wartość tego czynnika nie wynosi dokładnie 2 ze względu na oddziaływanie elektronu z próżnią („cząstkami wirtualnymi”), a jest równa w przybliżeniu g=2.0023. Wartość czynnika g w swobodnym atomie jest uzależniona od liczb spinowej i orbitalnej, co przy uwzględnieniu sprzężenia spinowo-orbitalnego można wyrazić równaniem:
Czynnik g, czyli czynnik Landégo lub żyromagnetyczny wynika z relatywistycznej mechaniki kwantowej, i w ogólności można go związać z różnicami w rozkładzie masy i ładunku w elektronie. Wartość tego czynnika nie wynosi dokładnie 2 ze względu na oddziaływanie elektronu z próżnią („cząstkami wirtualnymi”), a jest równa w przybliżeniu g=2.0023. Wartość czynnika g w swobodnym atomie jest uzależniona od liczb spinowej i orbitalnej, co przy uwzględnieniu sprzężenia spinowo-orbitalnego można wyrazić równaniem:
 W związku z tym energię pojedynczego elektron znajdującego się w polu magnetycznym można wyrazić równaniem: E=mjgμBH, w którym mj jest liczbą kwantową przyjmującą wartości J, J–1,…, –J. Takie ujęcie energii jednoznacznie implikuje fakt pojawienia się dwóch poziomów energetycznych. Otóż spin wypadkowy pojedynczego elektronu wynosi jak wiadomo S=1/2, liczba mj ma wartości równe ±1/2, a g = 2 gdy pominiemy wkład orbitalny, stąd wartości energii można wyrazić wzorem: E= ±μBH. Jak widać w polu magnetycznym pojawiają się dwa poziomy energii elektronu: niższy –½ + mB i wyższy ½ –mB; różnica energii pomiędzy nimi wynosi hν = 2μBH.
W związku z tym energię pojedynczego elektron znajdującego się w polu magnetycznym można wyrazić równaniem: E=mjgμBH, w którym mj jest liczbą kwantową przyjmującą wartości J, J–1,…, –J. Takie ujęcie energii jednoznacznie implikuje fakt pojawienia się dwóch poziomów energetycznych. Otóż spin wypadkowy pojedynczego elektronu wynosi jak wiadomo S=1/2, liczba mj ma wartości równe ±1/2, a g = 2 gdy pominiemy wkład orbitalny, stąd wartości energii można wyrazić wzorem: E= ±μBH. Jak widać w polu magnetycznym pojawiają się dwa poziomy energii elektronu: niższy –½ + mB i wyższy ½ –mB; różnica energii pomiędzy nimi wynosi hν = 2μBH.
>w stanie równowagi obsadzenie obydwu poziomów można wyrazić równaniami odpowiednio dla stanu o niższej energii:
 i wyższej energii:
i wyższej energii:
 Wartość β jest zależna od temperatury i wynosi β = 1/kT, gdzie k oznacza stałą Boltzmana. Rzut momentu magnetycznego na kierunek pola ma znak ujemny dla poziomu o wyższej energii i dodatni dla poziomu o niższej energii. W takim razie wypadkowe namagnesowanie próbki zawierającej N atomów w jednostce objętości wyraża się wzorem:
Wartość β jest zależna od temperatury i wynosi β = 1/kT, gdzie k oznacza stałą Boltzmana. Rzut momentu magnetycznego na kierunek pola ma znak ujemny dla poziomu o wyższej energii i dodatni dla poziomu o niższej energii. W takim razie wypadkowe namagnesowanie próbki zawierającej N atomów w jednostce objętości wyraża się wzorem:
 Wartość x w tym wyrażeniu jest równa x = μH/kT.
Wartość x w tym wyrażeniu jest równa x = μH/kT.
Moment orbitalny powoduje pojawienie się 2J +1 poziomów energii a jego uwzględnienie prowadzi do następującego wzoru na namagnesowanie: ![]() w którym x = gJμBH/kT, a Bj jest funkcją Brillouina wyrażoną wzorem:
w którym x = gJμBH/kT, a Bj jest funkcją Brillouina wyrażoną wzorem:
 Opierając się na własnościach funkcji tangens i cotangens hiperboliczny, w szczególności przyjmowania przez nie wartości zbliżonych odpowiednio do wartości argumentu w przypadku tangensa i granicy ciągu dla cotangensa i znacznie mniejszych od jedności wartości x, oraz wiedząc, że podatność magnetyczna jest ilorazem namagnesowania i pola magnetycznego możemy zapisać:
Opierając się na własnościach funkcji tangens i cotangens hiperboliczny, w szczególności przyjmowania przez nie wartości zbliżonych odpowiednio do wartości argumentu w przypadku tangensa i granicy ciągu dla cotangensa i znacznie mniejszych od jedności wartości x, oraz wiedząc, że podatność magnetyczna jest ilorazem namagnesowania i pola magnetycznego możemy zapisać:

W wyrażeniu tym ρ oznacza efektywną liczbę magnetonów Bohra wyrażoną zależnością:
![]() a zależność na stałą Curie powiązaną z efektywnym momentem magnetycznym opisuje wzór:
a zależność na stałą Curie powiązaną z efektywnym momentem magnetycznym opisuje wzór:
 Zgodnie z prawem Curie-Weissa opisywanym wzorem:
Zgodnie z prawem Curie-Weissa opisywanym wzorem:
 podatność magnetyczna jest zależna od temperatury, a wartość stałej Weissa θ daje się wyznaczyć graficznie z wykresu zależności 1/χ od temperatury.
podatność magnetyczna jest zależna od temperatury, a wartość stałej Weissa θ daje się wyznaczyć graficznie z wykresu zależności 1/χ od temperatury.
 Ponieważ podatność magnetyczna jest zależna od temperatury, a jednocześnie momenty spinowe i orbitalne powodują zniesienie degeneracji stanów to ich obsadzenie również będzie zależne od temperatury. Innymi słowy możemy wyróżnić trzy stany, w których odpowiednio pojawiają się multiplety o wartości rozszczepienia znacznie większej od wartości kT, małym w stosunku do kT i porównywalnej z kT (stan pośredni). W przypadku gdy energie hν pomiędzy rozszczepionymi multipletami znacznie przewyższają czynnik temperaturowy (kT) oczywistym jest, że obsadzenie stanu o najniższej energii będzie znaczące. W takim przypadku własności magnetyczne zależą jedynie od liczby kwantowej J. Sytuacja taka mam miejsce w przypadku pierwiastków f-elektronowych. W tabeli przedstawione zostały wartości obliczonego na podstawie równania zależnego od liczby kwantowej J i wyznaczonego momentu magnetycznego dla jonów lantanowców.
Ponieważ podatność magnetyczna jest zależna od temperatury, a jednocześnie momenty spinowe i orbitalne powodują zniesienie degeneracji stanów to ich obsadzenie również będzie zależne od temperatury. Innymi słowy możemy wyróżnić trzy stany, w których odpowiednio pojawiają się multiplety o wartości rozszczepienia znacznie większej od wartości kT, małym w stosunku do kT i porównywalnej z kT (stan pośredni). W przypadku gdy energie hν pomiędzy rozszczepionymi multipletami znacznie przewyższają czynnik temperaturowy (kT) oczywistym jest, że obsadzenie stanu o najniższej energii będzie znaczące. W takim przypadku własności magnetyczne zależą jedynie od liczby kwantowej J. Sytuacja taka mam miejsce w przypadku pierwiastków f-elektronowych. W tabeli przedstawione zostały wartości obliczonego na podstawie równania zależnego od liczby kwantowej J i wyznaczonego momentu magnetycznego dla jonów lantanowców.
| Konfiguracja f n | M3+ | term podstawowy | μobl | μexp (temperatura pokojowa) |
| 0 | La | 1S0 | 0 | diamagnetyk |
| 1 | Ce | 2F5/2 | 2,54 | 2,3 – 2,5 |
| 2 | Pr | 3H4 | 3,58 | 3,4 – 3,6 |
| 3 | Nd | 4I9/2 | 3,62 | 3,5 – 3,6 |
| 4 | Pm | 5I4 | 2,68 | – |
| 5 | Sm | 6H5/2 | 0,84 | 1,5 – 1,6 |
| 6 | Eu | 7F0 | 0 | 3,4 – 3,6 |
| 7 | Gd | 8S7/2 | 7,92 | 7,8 – 8,0 |
| 8 | Tb | 7F6 | 9,72 | 9,4 – 9,6 |
| 9 | Dy | 6H15/2 | 10,63 | 10,4 – 10,5 |
| 10 | Ho | 5I8 | 10,60 | 10,3 – 10,5 |
| 11 | Er | 4I15/2 | 9,57 | 9,4 – 9,6 |
| 12 | Tm | 3H6 | 7,63 | 7,1 – 7,4 |
| 13 | Yb | 2S7/2 | 4,50 | 4,4 – 4,9 |
| 14 | Lu | 1F0 | 0 | diamagnetyk |
Jak widać uwzględnienie jedynie stanu podstawowego daje bardzo dobrą zgodność obliczonych momentów magnetycznych z wartościami eksperymentalnymi dla wszystkich pierwiastków poza samarem i europem. W przypadku tych dwóch lantanowców niezbędnym jest uwzględnienie większej liczby stanów gdyż w ich przypadku różnica energetyczna pomiędzy podstawowym a wyższymi multipletami jest porównywalna z kT.
W sytuacji gdy wartość rozszczepienia multipletów jest mała w stosunku do czynnika temperaturowego, sprzężenie spinowo-orbitalne (LS) jest małe w porównaniu do oddziaływań L i S z; polem magnetycznym, a wzór na podatność magnetyczną przyjmuje postać:
 Najbardziej skomplikowaną jest sytuacja gdy energia rozszczepienia multipletów jest porównywalne co do wartości z czynnikiem temperaturowym. Oczywistym jest, że tutaj obsadzone są nie tylko multiplety o najniższej energii i należy uwzględnić przy obliczaniu podatności magnetycznej stopień obsadzenia wszystkich multipletów w zależności od temperatury. Wzór na podatność magnetyczną jest funkcją liczby J i temperatury:
Najbardziej skomplikowaną jest sytuacja gdy energia rozszczepienia multipletów jest porównywalne co do wartości z czynnikiem temperaturowym. Oczywistym jest, że tutaj obsadzone są nie tylko multiplety o najniższej energii i należy uwzględnić przy obliczaniu podatności magnetycznej stopień obsadzenia wszystkich multipletów w zależności od temperatury. Wzór na podatność magnetyczną jest funkcją liczby J i temperatury:
 Prawo Curie w takim przypadku nie jest spełnione. Sytuacja tego rodzaju ma miejsce w przypadku jonów metali d-elektronowych, w których sprzężenie spinowo-orbitalne jest „zaburzeniem” pola krystalicznego. Innymi słowy wpływ ligandów na elektrony d jest bardzo duży. Następuje w takim układzie „zamrożenie” momentu orbitalnego, a moment spinowy ma decydujący wpływ na właściwości magnetyczne. Opis kwantowo-mechaniczny takich układów został opracowany przez van Vlecka. Pomijając dość złożony aparat matematyczny możemy stwierdzić, że w rozpatrywanym przypadku pojawiają się dwa człony związane z paramagnetyzmem. Pierwszy z nich określa paramagnetyzm zależny od temperatury, a drugi wynikający z indukowanego magnetyzmu jest od temperatury niezależny. Odnosząc się do wyżej zamieszczonego rysunku możemy czynnik niezależny od temperatury powiązać z odcinkiem BC i określić go jako moment magnetyczny prostopadły do wektora J.
Prawo Curie w takim przypadku nie jest spełnione. Sytuacja tego rodzaju ma miejsce w przypadku jonów metali d-elektronowych, w których sprzężenie spinowo-orbitalne jest „zaburzeniem” pola krystalicznego. Innymi słowy wpływ ligandów na elektrony d jest bardzo duży. Następuje w takim układzie „zamrożenie” momentu orbitalnego, a moment spinowy ma decydujący wpływ na właściwości magnetyczne. Opis kwantowo-mechaniczny takich układów został opracowany przez van Vlecka. Pomijając dość złożony aparat matematyczny możemy stwierdzić, że w rozpatrywanym przypadku pojawiają się dwa człony związane z paramagnetyzmem. Pierwszy z nich określa paramagnetyzm zależny od temperatury, a drugi wynikający z indukowanego magnetyzmu jest od temperatury niezależny. Odnosząc się do wyżej zamieszczonego rysunku możemy czynnik niezależny od temperatury powiązać z odcinkiem BC i określić go jako moment magnetyczny prostopadły do wektora J.
Dla jonów pierwiastków d–elektronowych wyznaczone eksperymentalnie oraz obliczone wartości podatności magnetycznej przedstawione zostały w poniższej tabeli.
| jon | term podstawowy | eksperyment | |||
| Ti3+ | 2D3/2 | 3,00 | 1,55 | 1,73 | 1,7 – 1,8 |
| Ti2+, V3+ | 3F2 | 4,47 | 1,63 | 2,83 | 2,7 – 2,9 |
| V2+, Cr3+ | 4F3/2 | 5,20 | 0,70 | 3,87 | 3,7 – 3,9 |
| Cr2+, Mn3+ | 5D0 | 5,48 | 0 | 4,90 | 4,8 – 4,9 |
| Mn2+, Fe3+ | 6S5/2 | 5,92 | 5,92 | 5,92 | 5,7 – 6,0 |
| Fe2+, Co3+ | 5D4 | 5,48 | 6,71 | 4,90 | 5,0 – 5,6 |
| Co2+ | 4F9/2 | 5,20 | 6,63 | 3,87 | 4,3 – 5,2 |
| Ni2+ | 3F4 | 4,47 | 5,59 | 2,83 | 2,9 – 3,5 |
| Cu2+ | 2D5/2 | 3,00 | 3,55 | 1,73 | 1,8 – 2,1 |
Uwzględnienie jedynie spinu daje wyniki o dobrej zgodności z eksperymentem zwłaszcza dla lżejszych pierwiastków. Jednak dane te dotyczą swobodnych jonów, a jak wiadomo na właściwości magnetyczne związków koordynacyjnych ma wpływ geometria całego układu.
Uwzględnienie teorii pola krystalicznego pozwala na przewidywanie, w których przypadkach czynnik orbitalny będzie odgrywał rolę w wypadkowym magnetyzmie związku. Jak wiadomo rozszczepienie orbitali d atomu centralnego w polach krystalicznych o symetrii oktaedrycznej czy tetraedrycznej prowadzi do pojawienia się dwóch poziomów odpowiednio trój– i dwukrotnie zdegenerowanych. Elektrony obsadzające poziom t2(g) czy e(g) w różnym stopniu oddziałują z ligandami, co ma wpływ na udział momentu orbitalnego w momencie magnetycznym związku. Już sama zmiana degeneracji ma istotny wpływ na udział momentu orbitalnego. W przypadku orbitali d musimy powiązać moment orbitalny z „przekształceniem” jednego orbitalu w drugi poprzez operacje symetrii. W związku z tym orbitale dxy, dxz i dyz mogą przekształcać się pomiędzy sobą poprzez obrót wokół odpowiedniej osi o kąt 90o. Podobnie dxy przekształcony wokół osi z o kąt 45o przekształca się w dx2-y2. Sytuacja taka ma oczywiście miejsce w przypadku swobodnego jonu, a w związku koordynacyjnym o określonej symetrii (np. Oh) właśnie obniżenie degeneracji powoduje zahamowanie procesu zamiany orbitali dxy i dx2-y2, a poziom e(g) tworzony jest przez orbitale, które nie mają możliwości wzajemnej zamiany ze względu na symetrię, i co za tym idzie nie mają wpływu na orbitalny moment magnetyczny. Nie bez znaczenia jest też wielkość parametru rozszczepienia, która jest skorelowana z występowaniem układów nisko- i wysokospinowych. Biorąc pod uwagę powyższe uwagi można określić, że dla niskospinowych związków okatedrycznych udział momentu orbitalnego występuje dla konfiguracji t2g4 i t2g5, a dla t2g6 i t2g6eg1 spodziewamy się jego braku. Dla wysokospinowych związków oktaedrycznych moment orbitalny odgrywa rolę dla konfiguracji t2g1 i t2g2 i dla t2g4eg2 i t2g5eg2. Natomiast w momencie magnetycznym wysokospinowych cząsteczek o geometrii oktaedrycznej i konfiguracjach: t2g3, t2g3eg1, t2g3eg2, t2g6eg2 i t2g6eg3 wkład momentu orbitalnego jest zerowy. Dla związków tetraedrycznych nie występują konfiguracje niskospinowe (parametr rozszczepienia tetraedru to 4/9Do) i biorąc pod uwagę zmianę poziomów t2 i e można oczekiwać, że dla konfiguracji e2t21, e2t22 oraz e4t24, e4t25 moment orbitalny będzie widoczny w magnetyzmie cząsteczki, a dla e1, e2, e2t21, e2t23, e2t21, e3t23 i e4t23 nie będzie odgrywał żadnej roli.
Rozpatrując konfiguracje elektronowe atomu centralnego w związkach koordynacyjnych powinniśmy posługiwać się termami zamiast orbitalami d. Ponieważ termy mogą wzajemnie oddziaływać, co znajduje swoje odbicie we wpływie orbitalnego momentu pędu na moment magnetyczny cząsteczki. W takim wypadku wartość momentu magnetycznego można powiązać z momentem uwzględniającym tylko spin (μs) oraz parametrem rozszczepienia 10Dq, wzorem:
 w którym λ oznacza wartość sprzężenia spinowo-orbitalnego pomiędzy oddziałującymi termami (α przyjmuje różne wartości w zależności do rodzaju termu, odpowiednio 2 dla termów typu E, 4 dla A). Istotnym jest, ze wartość λ ma związek ze stałą sprzężenia-spinowo orbitalnego pojedynczego elektronu w danym atomie centralnym, co można wyrazić jako:
w którym λ oznacza wartość sprzężenia spinowo-orbitalnego pomiędzy oddziałującymi termami (α przyjmuje różne wartości w zależności do rodzaju termu, odpowiednio 2 dla termów typu E, 4 dla A). Istotnym jest, ze wartość λ ma związek ze stałą sprzężenia-spinowo orbitalnego pojedynczego elektronu w danym atomie centralnym, co można wyrazić jako:
 Wyrażenie to jest spełnione dla związków koordynacyjnych z ligandami silnego pola, dla których wartość S określa dość dokładnie term podstawowy układu.
Wyrażenie to jest spełnione dla związków koordynacyjnych z ligandami silnego pola, dla których wartość S określa dość dokładnie term podstawowy układu.
<td">
| Oh słabe pole | Oh silne pole | Td silne pole | ||||||
| jon | ζ | d n | term | λ | term | λ | term | λ |
| Ti3+ | 155 | 1 | 2T2g | +155 | 2T2g | +155 | 2E | +155 |
| V3+ | 210 | 2 | 2T1g | +105 | 2T1g | +105 | 3A2 | +105 |
| V2+ | 170 | 3 | 4A2g | +57 | 4A2g | +57 | 4T1 | +57 |
| Cr3+ | 275 | 3 | 4A2g | +92 | 4A2g | +92 | 4T1 | +92 |
| Cr2+ | 230 | 4 | 5Eg | +58 | 3T1g | –115 | 5T2 | +58 |
| Mn3+ | 355 | 4 | 5Eg | +89 | 3T1g | –178 | 6A1 | – |
| Mn2+ | 300 | 5 | 6A1g | – | 2T2g | –300 | 6A1 | – |
| Fe3+ | 460 | 5 | 6A1g | – | 2T2g | –460 | 6A1 | – |
| Fe2+ | 400 | 6 | 5T2g | –100 | 1A1g | – | 5E | –100 |
| Co3+ | 580 | 6 | 5T2g | –145 | 1A1g | – | 4A2 | –172 |
| Co2+ | 515 | 7 | 4T1g | –172 | 2Eg | –515 | 4A2 | –238 |
| Ni3+ | 715 | 7 | 4T1g | –213 | 2Eg | –715 | 4A2 | –238 |
| Ni2+ | 630 | 8 | 3A2g | –315 | 3A2g | –315 | 3T1 | –315 |
| Cu2+ | 830 | 9 | 2Eg | –830 | 2Eg | –830 | 2T2 | –830 |
Sytuacja staje się bardziej skomplikowana przy uwzględnieniu sprzężenia spinowo-orbitalnego dla termów typu T. Weźmy pod uwagę konfigurację d 1 i odpowiadający jej term podstawowy swobodnego jonu w polu oktaedrycznym czyli 2D. Całkowity stopień degeneracji tego termu wynosi 10, przy uwzględnieniu sprzężeń spinowego i orbitalnego (2S+1)(2L+1). Pole oktaedryczne powoduje zmianę degeneracji i utworzenie dwóch poziomów 2Eg i 2T2g. Degeneracja niżej energetycznego poziomu jest następnie zmieniana przez sprzężenie spinowo-orbitalne, efekt Zeemana pierwszego rzędu, zewnętrzne pole magnetyczne (pomiar podatności wykonywany jest w polu magnetycznym) i ostatecznie przez efekt Zeemana drugiego rzędu. Uwzględnienie tych oddziaływań prowadzi do wzorów podanych poniżej:
| konfiguracja | λ | term | μ2= |
| słabe pole | |||
| d 1 (oktaedr) | +ζ | 2T2 |  |
| d 9 (tetraedr) | –ζ | ||
| d 2 (oktaedr) | +ζ/2 | 3T1 |  |
| d 2 (tetraedr) | +ζ/2 | ||
| d 6 (oktaedr) | –ζ/4 | 3T2 |  |
| d 6 (tetraedr) | +ζ/4 | ||
| d 7 (oktaedr) | ζ/3 | 4T1 |  |
| d 7 (tetraedr) | +ζ/4 | ||
| silne pole | |||
| d 1 (oktaedr) | +ζ | 2T2 |  |
| d 5 (oktaedr) | –ζ | ||
| d 2 (oktaedr) | +ζ/2 | 3T1 |  |
| d 4 (oktaedr) | +ζ/2 |
W powyższych wzorach x = λ/kT.
zewnętrzne pole magnetyczne powoduje zniesienie degeneracji poziomów energetycznych proporcjonalnie do natężenia pola magnetycznego. Jest to efekt Zeemana pierwszego rzędu, a symetryczne rozszczepienie poziomów energetycznych odpowiada orientacji jonów w zewnętrznym polu i oczywiście orientacji samego pola. Innymi słowy efekt pierwszego rzędu zmienia degenerację poziomów nie zmieniając średniej energii poziomu zdegenerowanego czyli następuje rozszczepienie „symetryczne” względem energii poziomu wyjściowego. Natomiast zmiana energii, proporcjonalna do kwadratu natężenia pola magnetycznego, powoduje zaburzenie energii stanu podstawowego poprzez mieszanie termów podstawowego i wyższych. Obniżenie energii stanu podstawowego jest proporcjonalne do H 2. Schemat poniższy przedstawia wpływ poszczególnych czynników na degenerację poziomów energetycznych w przypadku jonu o konfiguracji d 1 łącznie z wartościami energii poszczególnych poziomów.
 Obsadzenie rozszczepionych poziomów energetycznych jest uzależnione od temperatury. Jednak należy mieć na uwadze, że wpływ czynnika temperaturowego będzie zależny od energii rozkładu termów. Dla przykładu weźmy dwa jony lantanowców. Z jednej strony jon europu(III) o konfiguracji f 6, dla którego term podstawowy 7F0 jest niżej energetyczny od tripletowego stanu 7F1 przy czym różnica energii wynosi tylko około 0.03 eV co odpowiada przesunięciu pasm na widmach absorpcyjnych o 250 cm–1. W takim wypadku tylko w niskich temperaturach decydującą rolę odgrywa niezależny od temperatury efekt Zeemana drugiego rzędu, w temperaturach wyższych obsadzenie stanu 7F1 ma istotny wpływ na własności magnetyczne jonu Eu3+. Inaczej sytuacja wygląda dla jonu Sm3+ o konfiguracji f 3. W tym wypadku pierwszy wzbudzony stan 6H7/2 ma energię wyższą o 0.12 eV (1000 cm–1) od podstawowego termu 6H5/2. W takim wypadku efekt Zeemana drugiego rzędu nie wykazuje zależności od obsadzenia stanów wzbudzonych pojawiających się wraz ze wzrostem temperatury. Paramagnetyzm takiego jonu jest określany jako niezależny od temperatury paramagnetyzm van Vlecka. Sytuacja taka występuje w przypadku związków koordynacyjnych metali przejściowych, dla których rozszczepienie w polu ligandów jest z reguły na tyle silne, że wpływ temperatury na własności magnetyczne jonów jest widoczny dopiero w stosunkowo wysokich temperaturach, gdzie własności paramagnetyczne są stosunkowo niewielkie. Jednak należy mieć na uwadze fakt, że taki stan jest zależny również od rodzaju termu podstawowego.
Obsadzenie rozszczepionych poziomów energetycznych jest uzależnione od temperatury. Jednak należy mieć na uwadze, że wpływ czynnika temperaturowego będzie zależny od energii rozkładu termów. Dla przykładu weźmy dwa jony lantanowców. Z jednej strony jon europu(III) o konfiguracji f 6, dla którego term podstawowy 7F0 jest niżej energetyczny od tripletowego stanu 7F1 przy czym różnica energii wynosi tylko około 0.03 eV co odpowiada przesunięciu pasm na widmach absorpcyjnych o 250 cm–1. W takim wypadku tylko w niskich temperaturach decydującą rolę odgrywa niezależny od temperatury efekt Zeemana drugiego rzędu, w temperaturach wyższych obsadzenie stanu 7F1 ma istotny wpływ na własności magnetyczne jonu Eu3+. Inaczej sytuacja wygląda dla jonu Sm3+ o konfiguracji f 3. W tym wypadku pierwszy wzbudzony stan 6H7/2 ma energię wyższą o 0.12 eV (1000 cm–1) od podstawowego termu 6H5/2. W takim wypadku efekt Zeemana drugiego rzędu nie wykazuje zależności od obsadzenia stanów wzbudzonych pojawiających się wraz ze wzrostem temperatury. Paramagnetyzm takiego jonu jest określany jako niezależny od temperatury paramagnetyzm van Vlecka. Sytuacja taka występuje w przypadku związków koordynacyjnych metali przejściowych, dla których rozszczepienie w polu ligandów jest z reguły na tyle silne, że wpływ temperatury na własności magnetyczne jonów jest widoczny dopiero w stosunkowo wysokich temperaturach, gdzie własności paramagnetyczne są stosunkowo niewielkie. Jednak należy mieć na uwadze fakt, że taki stan jest zależny również od rodzaju termu podstawowego.
Siła pola ligandów może być mniejsza niż inne oddziaływania, i w takim przypadku można traktować atom centralny związku koordyancyjnego jak wolny jon. Przypadek taki (dużych rozszczepień multipletów) występuje dla jonów lantanowców. Pole ligandów może być silniejsze niż oddziaływanie spinowo-orbitalne, ale słabsze od innego rodzaju oddziaływań i wtedy mamy do czynienia ze słabym polem ligandów. Kolejny rodzaj pola można wyróżnić gdy jego siła jest większa od sprzężenia orbitalnego i spinowo-orbitalnego ale mniejsza niż oddziaływanie spinowe. W tym pośrednim polu ligandów reguła Hunda mówiąca o uprzywilejowaniu najwyższej multipletowości układu zostaje złamana, a multipletowość układu „rozgranicza się” na odrębne poziomy t2g i eg (oktaedr). Ostatni przypadek, silnego pola gdy wszystkie inne oddziaływania są słabsze niż pole ligandów charakteryzuje się złamaniem pierwszej reguły Hunda i stany ze sparowanymi elektronami mają niższą energię niż stany o niesparowanych spinach. Zmiany energii termów w zależności od siły pola dobrze przedstawiają diagramy Tanabe-Sugano i dla konfiguracji d 4, d 5, d 6 i d 7przy pewnej sile pola ligandów następuje sparowanie spinów.
W przypadku związków koordynacyjnych metali czwartego i piątego okresu częściej niż dla związków koordynacyjnych jonów 3d-elektronowych spotyka się układy diamagnetyczne. Z jednej strony można powiązać ten fakt z większym oddziaływaniem orbitali d atomu centralnego z ligandami (większy efekt nefeloauksetyczny). Ponadto dla pierwiastków drugiego i trzeciego okresu wartości stałej sprzężenia spinowo-orbitalnego są znacznie większe niż w przypadku pierwiastków 3d-elektronowych.
| konfiguracja | jon | ζ | term podstawowy | λ |
| 4d 2 | Mo(IV) | 850 | 3T1g | +425 |
| 4d 3 | Mo(III) | 800 | 4A2g | +267 |
| 4d 4 | Ru(IV) | 1400 | 3T1g | –700 |
| 4d 5 | Ru(III) | 1250 | 3T2g | –1250 |
| Rh(IV) | 1700 | –1700 | ||
| 5d 2 | W(IV) | 2300 | 3T1g | +1150 |
| Re(V) | 3700 | +1850 | ||
| 5d 3 | W(III) | 1800 | 4A2g | +600 |
| Re(IV) | 3300 | +1100 | ||
| 5d 4 | Re(III) | 2500 | 3T1g | –1250 |
| Os(IV) | 4000 | –2000 | ||
| Ir(V) | 5000 | –2750 | ||
| 5d 5 | Os(III) | 3000 | 3T2g | –3000 |
| Ir(IV) | 5000 | –5000 |
W rozważanych powyżej układach właściwości magnetyczne odpowiadały izolowanym centrom paramagnetycznym. Taka sytuacja jest częsta w przypadku związków koordynacyjnych gdyż diamagnetyczne ligandy otaczające jony centralne rzeczywiście powodują brak wzajemnych oddziaływań magnetycznych w próbce. Ale istnieją układy koordynacyjne, w których momenty magnetyczne poszczególnych centrów oddziałują ze sobą czy to za sprawą odpowiednio krótkich odległości pomiędzy nimi w sieci krystalicznej, czy też dzięki przenoszeniu oddziaływań poprzez odpowiednie ligandy. Zaniedbując orbitalny moment magnetyczny jonów, oddziaływanie to można opisać wyrażeniem: ΔE=2JSiSk, w którym J oznacza stałą sprzężenia wymiany i nie odpowiada kwantowej liczbie J. Dodatnia wartość J oznacza, że spiny oddziałujących centrów paramagnetycznych są ustawione w tym samym kierunku, a ujemna wskazuje na sparowanie spinów. W pierwszym przypadku mamy do czynienia z ferromagnetyzmem, a w drugim z antyferromagnetyzmem. Obydwa typy oddziaływań, ferromagnetyczne i antyferromagnetyczne, wykazują odpowiednią zależność temperaturową.
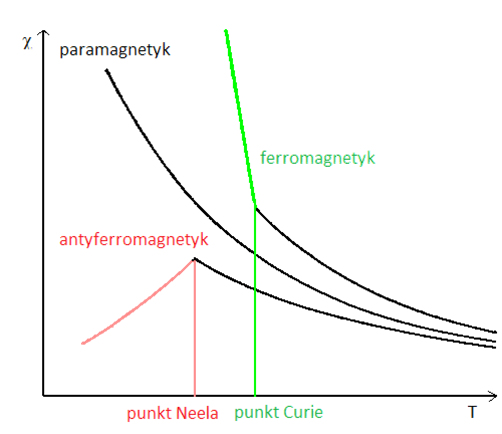 Zmiany podatności magnetycznej w zależności od temperatury dla różnych substancji magnetycznychAntyferromagnetyzm jest dość częstym zjawiskiem spotykanym w przypadku związków koordynacyjnych. Weźmy pod uwagę bimetaliczny, dwujądrowy związek koordynacyjny, w którym obydwa jony centralne są paramagnetyczne. Każdy z jonów centralnych posiada spinowy moment magnetyczny (S), a całkowity moment magnetyczny związku to S`. Całkowity moment S` przyjmuje wartości od 0 do 2S, czyli 2S+1 wartości. Każda z tych wartości definiuje odrębny poziom energetyczny, z których każdy wykazuje multipletowość równą 2S`+1, i posiada energię wyrażoną wzorem J[S`(S`+1)], gdzie J oznacza stałą sprzężenia. (często wartość stałej J jest definiowana jako wartość podwojona i wtedy energia jest wyrażana wzorem 1/2J[S`(S`+1)]) Ujemna wartość stałej J oznacza, że mamy do czynienia z oddziaływaniem antyferromagnetycznym. Poziom podstawowy definiowany jest przez S`=0, a najwyżej energetyczny poziom S`=2S. W przypadku ferromagnetyzmu, gdzie spiny są równoległe poziom podstawowy to S`=2S. Rozkład poziomów energetycznych układu antyferromagnetyczngo przedstawiony jest na rysunku:
Zmiany podatności magnetycznej w zależności od temperatury dla różnych substancji magnetycznychAntyferromagnetyzm jest dość częstym zjawiskiem spotykanym w przypadku związków koordynacyjnych. Weźmy pod uwagę bimetaliczny, dwujądrowy związek koordynacyjny, w którym obydwa jony centralne są paramagnetyczne. Każdy z jonów centralnych posiada spinowy moment magnetyczny (S), a całkowity moment magnetyczny związku to S`. Całkowity moment S` przyjmuje wartości od 0 do 2S, czyli 2S+1 wartości. Każda z tych wartości definiuje odrębny poziom energetyczny, z których każdy wykazuje multipletowość równą 2S`+1, i posiada energię wyrażoną wzorem J[S`(S`+1)], gdzie J oznacza stałą sprzężenia. (często wartość stałej J jest definiowana jako wartość podwojona i wtedy energia jest wyrażana wzorem 1/2J[S`(S`+1)]) Ujemna wartość stałej J oznacza, że mamy do czynienia z oddziaływaniem antyferromagnetycznym. Poziom podstawowy definiowany jest przez S`=0, a najwyżej energetyczny poziom S`=2S. W przypadku ferromagnetyzmu, gdzie spiny są równoległe poziom podstawowy to S`=2S. Rozkład poziomów energetycznych układu antyferromagnetyczngo przedstawiony jest na rysunku:
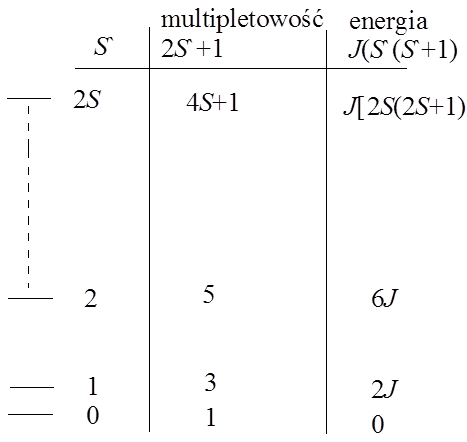 Multipletowość i energie poziomów w dwujądrowcyh związkach koordynacyjnych z oddziaływaniem antyferromagnetycznymPodatność magnetyczna takiego układu jest opisywana równaniem van Vlecka, przy czym rozkład multipletów na skali energii jest porównywalny z wartością czynnika temperaturowego kT. Odpowiednie równanie ma postać:
Multipletowość i energie poziomów w dwujądrowcyh związkach koordynacyjnych z oddziaływaniem antyferromagnetycznymPodatność magnetyczna takiego układu jest opisywana równaniem van Vlecka, przy czym rozkład multipletów na skali energii jest porównywalny z wartością czynnika temperaturowego kT. Odpowiednie równanie ma postać:
 Efekt Zeemana pierwszego rzędu powoduje rozszczepienie poziomu na 2S`+1 poziomów o energiach w zakresie od -gβHS` do +gβHS`, a tym samym czynnik E2i(1)/kT można wyrazić za pomocą
Efekt Zeemana pierwszego rzędu powoduje rozszczepienie poziomu na 2S`+1 poziomów o energiach w zakresie od -gβHS` do +gβHS`, a tym samym czynnik E2i(1)/kT można wyrazić za pomocą

W przypadku gdy cząsteczka składa się z dwóch różnych centrów paramagnetycznych, wtedy wzory się komplikują przez konieczność określenia wartości S` z szeregu Si-Sk do Si+Sk. Wartość czynnika g, który dla momentu czysto spinowego wynosi 2, jest zależna od wkładu momentu orbitalnego. Jeżeli następuje mieszanie termów podstawowego z wyższymi, czynnik g będzie niezależny od temperatury, ale nadal jego wartość będzie różna od 2. Przykładami związków, w których mamy do czynienia z wzajemnym oddziaływaniem centrów paramagnetycznych są octany miedzi(II) i chromu(II) o ogólnym wzorze [M2(CH3COO)4].
 W tych octanach (uwodnionych lub bezwodnych) następuje wzajemne oddziaływanie atomów centralnych, w przypadku octanu miedzi(II) poprzez orbitale dx2-y2, a w octanie chromu(II) również poprzez dxz, dyz i dz2.
W tych octanach (uwodnionych lub bezwodnych) następuje wzajemne oddziaływanie atomów centralnych, w przypadku octanu miedzi(II) poprzez orbitale dx2-y2, a w octanie chromu(II) również poprzez dxz, dyz i dz2.